Demostrar que la siguiente función tiene una única solución
$$\begin{align}&\text{Demostrar que la función}\ x^2=8lnx \ \text{tiene una única solución.}\end{align}$$
·
·
¡Hola Maar!
Será la ecuación la que tiene una sola solución.
Como sabrás, esa ecuación no se puede resolver algebraicamente, pero tenemos algunas técnicas y teoremas que nos pueden ayudar a determinar que solo hay una solución.
Tomemos la función:
f(x) = x^2 - 8·ln x
Las saluciones de la ecuación son los puntos donde f(x)=0
Para empezar la función está definida solo para x>0 ya que si no el logaritmo no estaría definido.
Vamos a calcular la derivada
f'(x) = 2x - 8/x
veamos donde corta al eje X
2x - 8/x = 0
2x^2 - 8 = 0
2x^2 = 8
x^2=4
x=2
el -2 no nos sirve pues ya dijimos que la función solo está definida en x>0
En el intervalo (0,2) la derivada es negativa, toma por ejemplo x=1 y tendrás
f'(1) = 2·1 - 8/1 = -6
Y en el intervalo(2, infinito) es positiva, por ejemplo para x=4
f'(4) = 2·4 - 8/4 = 8-2 = 6
Luego la función es decreciente hasta x=2 y creciente después.
Veamos el valor de la función en x=0, mejor dicho, el límite
lim x->0 f(x) = 0^2 - 8ln(0) = -(-infinito) = infinito
Veamos el valor en x=2
f(2) = 2^2 - 8·ln(2) = 4 - 5.545177 = -1.545177
Y el límite en infinito es
lim x-->inf f(x) = inf
Pues lo siento mucho pero el enunciado miente, hay dos respuestas, aquí tienes la gráfica
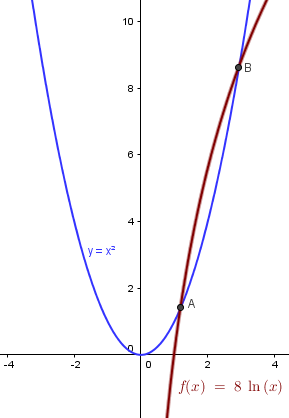
Las dos respuestas aproximadamente son
x=1.1957
x=2.9348
·
Y eso es todo, sa lu dos.
:
:
