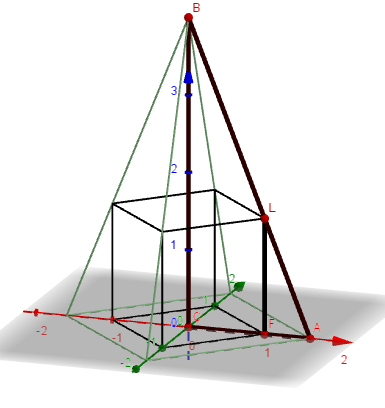
La razón del volumen v1 de la pirámide con respecto al volumen v2 del cubo inscrito en la pirámide, si se sabe que h igual 2a
Un cubo esta inscrito en una pirámide regular cuadrangular de altura h y lado de la base a, cuatro vértices pertenecen a las aristas laterales de la pirámide. Encuentre la razón del volumen v1 de la pirámide con respecto al volumen v2 del cubo inscrito en la pirámide, si se sabe que h igual 2a
2 respuestas
Respuesta de Valero Angel Serrano Mercadal
2
Respuesta de Lucas m
1