Encontrar en qué punto alcanzó su altura máxima, también determinar los puntos en donde fue lanzada, así como el punto en donde
Una bala se dispara desde el piso formando un trayectoria tipo parábola, donde su ecuación
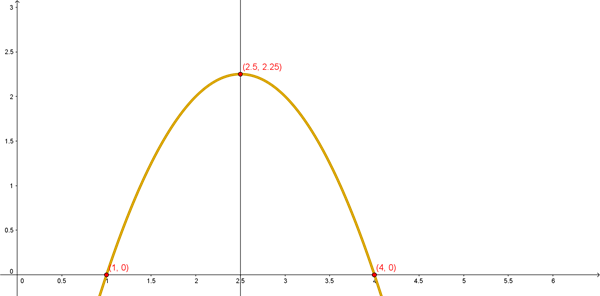
es y = -x 2 + 5x -4,
Encontrar en qué punto alcanzó su altura máxima, también determinar los
Puntos en donde fue lanzada, así como el punto en donde cayó.
Son todos los detalles, quiero saber el procedimiento, entiendo que es una parábola para abajo, pero quiero conocer el proceso para hacerlo
Respuesta de Lucas m
7
1 respuesta más de otro experto
Respuesta de Valero Angel Serrano Mercadal
4


Gracias por su aportación - Adriana Martinez Lira
Buenas noches Mtro. Lucas...¿Cómo puedo hacer la gráfica en Excel que usted presenta? - PeAr JeMa
Yo la hago con GeoGebra.Programa libre que te puedes descargar o trabajar online en GeoGebra.org - Lucas m
Graficar com Excel aquí tienes una explicación para hacerlo con Excel;);) - Lucas m