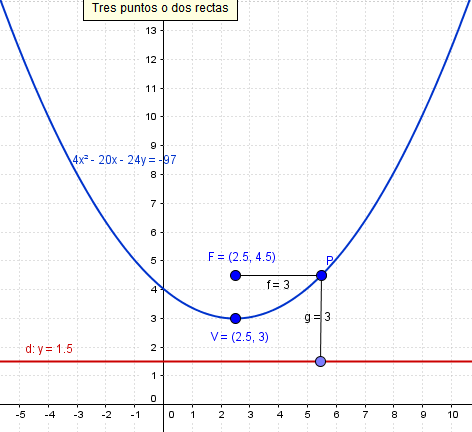
Demostrar que la ecuación representa una parábola. Determine: vértice, foco y directriz
Agradezco su ayuda con la solución de este ejercicio:
Demostrar que la ecuación representa una parábola. Determine: vértice, foco y directriz

2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta de Lucas m
1