Tengo dudas sobre este ejercicio de funciones
1. Lee y analiza el planteamiento. Analiza el siguiente problema y de acuerdo con lo que has revisado en las unidades anteriores, desarrolla y responde el planteamiento, además explicar tu solución paso a paso.

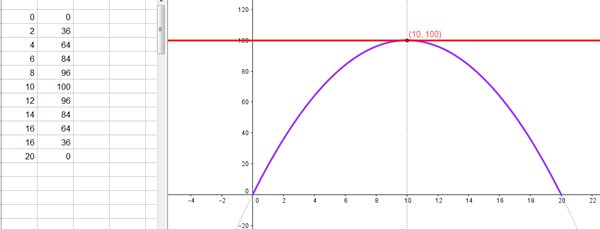
2. Realiza el bosquejo de la gráfica que representa la ecuación y con ayuda de la gráfica responde las siguientes preguntas:
a) ¿Cuál es el punto máximo del número de tapas que se recolectan, así como el tiempo en el que ya no recolectan nada? (No olvides que los resultados son en miles)
b) ¿Cuál es la relación que existe entre el tiempo y el número de tapas que se juntaron y cuál sería el total de tapas en punto máximo en conjunto con lo ya obtenido por la asociación con anterioridad?
Para incluir la gráfica en tu presentación puedes usar la cámara de tu celular y tomar una fotografía. Es importante que recuerdes que la gráfica debe ser elaborada a mano mediante el proceso revisado en el tema de “Funciones” de la semana 1.
3. Obtén la ecuación de la recta secante a partir de la derivada de la función y el valor de su pendiente, intégrala en la misma gráfica anterior y para este caso, incorpora un audio en el que des tu respuesta a la siguiente pregunta, iniciando con tu nombre y grupo al que perteneces:
c) Qué relación existe entre el punto máximo alcanzado y la recta secante y su pendiente; relaciónalo con los datos obtenidos en tu actividad.

Muchas gracias pero esta un poco incompleta. Faltaría el desarrollo de la pregunta b completa y su gráfica. Necesito por favor Los pasos para obtener la recta secante y su pendiente. Integrar la gráfica de la función principal y la recta secante y su pendiente, explicando la relación que existe entre estas dos (secante y su pendiente)Muchas gracias - Nancy Vargas
Profe y Qué relación existe entre el punto máximo alcanzado y la recta secante y su pendiente; relaciónalo con los datos obtenidos en tu actividad. - Anónimo
Perdón, ¿se podría hacer este ejercicio con una recta secante? o ¡cuales son los motivos por los cuales no se puede realizar? Muchas gracias - Carlos Atenco