;)
Hola Efrain!
Valora las respuestas con Excelente, yo no me evaluo esta es una actividad altruista.
Como la otra demostración con vectores, parece que no la entendiste, te hago esta usando la trigonometria.
Sea el paralelogramo ABCD. Como todos los paralelogramos tiene los lados y los ángulos iguales dos a dos
AB=DC
AD=BC
Aplicando el teorema del coseno a la mitad del paralelogramo que coge cada una de las diagonales:
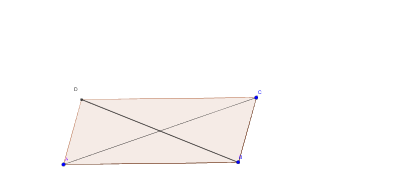
En el triángulo ABC:
$$\begin{align}&AC^2=AB^2+BC^2-2·AB·BC·cosB\\&\\&en \ el \ triángulo\ ADB:\\&BD^2=AB^2+AD^2-2·AB·AD·cosA\\&\\&Los \ cuatro \ angulos \ paralelogramo \ suman \ 360º\ y \ son \ iguales \ dos \ a \ dos:\\&A=C\\&B=D\\&2A+2B=360º\\&\\&A+B=180º\Rightarrow A \ y \ B \ son \ suplementarios\\&los \ cosenos \ de \ dos \ ángulos \ suplementarios \ son \ opuestos\\&luego \\&cosB=-cosA\\&sumando \ las \ dos \ igualdades \ inciales:\\&AC^2+BD^2=AB^2+BC^2-2·AB·BC·cosB+AB^2+AD^2-2·AB·AD·cosA\\&AC^2+BD^2=AB^2+BC^2+AB^2+AD^2-2·AB·BC(-cosA)-2AB·AC·cosA\\&AC^2+BD^2=AB^2+BC^2+CD^2+AD^2+2·AB·BCcosA-2AB·AC·cosA\\&\\&AC^2+BD^2=AB^2+BC^2+CD^2+AD^2\\&\\&\\&\\&\end{align}$$

