Calcula todos los valores de z para los que:
A)(z^4+3z-2)^2-(2z^2-z+1)^2=0
B)z^6+z^5+z^4+z^3+z^2+z+1=0
C)z^6+64=0
2 respuestas
Respuesta de Lucas m
1
;)
Hola Miriam!
C)
$$\begin{align}&z^6=-64\\&\\&z= \sqrt [6]{64_{180º}}=2_{\alpha}\\&\\&\alpha=\frac{180º+k360º}{6}\\&\\&k=0 \rightarrow \alpha_1 =30º\Rightarrow z_1=2 (cos30º+isen30º)\\&k=1 \rightarrow \alpha_2=90º\rightarrow2i\\&\\&k=2 \rightarrow \alpha_3 =150º \rightarrow 2(\cos 150º +isen 150º)\\&\\&210º\rightarrow 2 (\cos 210º+isen 210º)\\&\\&270º \rightarrow -2i\\&\\&330º\\&\\&\end{align}$$;)
;)
Respuesta de Valero Angel Serrano Mercadal
1
Ya veo que te hicieron el C.
El A parece bastante complicado, a lo mejor luego no lo es, pero la primera apariencia es mala, conviene que lo mandes en otra pregunta.
El segundo se puede hacer si conocemos la igualdad ciclotómica:
$$\begin{align}&a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+...+a·b^{n-2}+b^{n-1})\\&\\&\text{Haciendo}\\&a=z\\&b=1\\&n=7\\&\\&z^7-1=(z-1)·(z^6+z^5+z^4+z^3+z^2+z+1)\\&\\&z^6+z^5+z^4+z^3+z^2+z+1=\frac{z^7-1}{z-1}=0\implies\\&\\&z^7-1=0 \quad y\quad z \neq 1\\&\\&z^7=1\\&\\&\text{Son las raíces septimas de 1 salvo el 1}\\&\\&z_1=\cos \frac{2\pi}{7}+ i ·sen \frac{2\pi}{7}\\&\\&z_2=\cos \frac{4\pi}{7}+ i ·sen \frac{4\pi}{7}\\&\\&z_3=\cos \frac{6\pi}{7}+ i ·sen \frac{6\pi}{7}\\&\\&z_4=\cos \frac{8\pi}{7}+ i ·sen \frac{8\pi}{7}\\&\\&z_5=\cos \frac{10\pi}{7}+ i ·sen \frac{10\pi}{7}\\&\\&z_6=\cos \frac{12\pi}{7}+ i ·sen \frac{12\pi}{7}\end{align}$$Y para hacer una comprobación he tomado uno de ellos y lo he calculado con WolframAlpha:
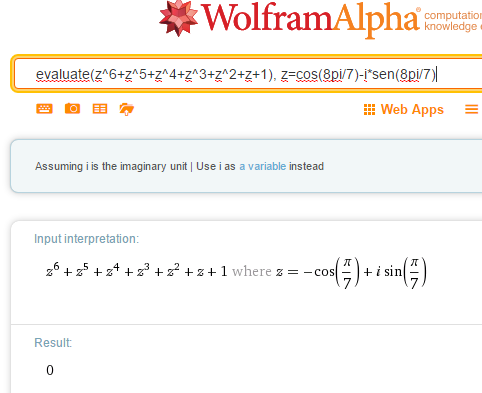
Pero por si nos fiáramos le doy los valores del seno y coseno con calculadora
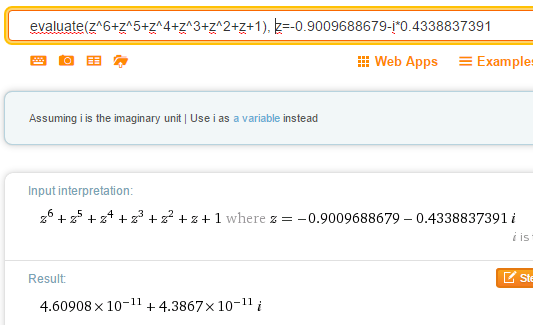
No da cero exacto pero como si lo fuese, es muy difícil que una operación con complejos elevados a semejantes potencias de 0 de mejor aproximación cuando lo que hemos dado nosotros no eran los valores exactos.
Y eso es todo, saludos.
:
: