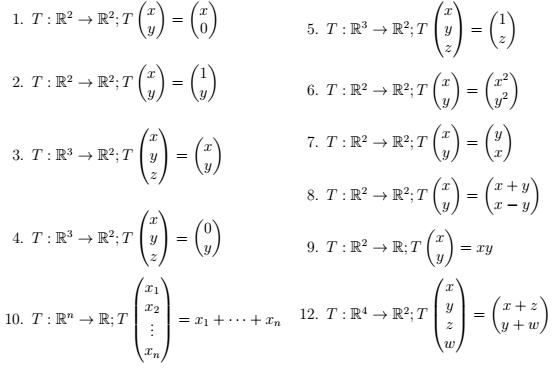¿Saber si es transformación lineal?
He consultado varias fuentes y no comprendo bien por que método puedo verificar esto.
2 respuestas
·
·
¡Hola Antonio!
El método es probando las dos propiedades:
f(a+b) = f(a)+f(b)
f(ka) = k·f(a)
Y así podrías hacer todos los que quedan.
Pero las aplicaciones lineales ya están mas que estudiadas y se sabe como es su forma
$$\begin{align}&\text{Una aplicacin lineal es}\\&f:\mathbb R^n \to \mathbb R\\&\\&f(x_1,x_2,x_3,...,x_n)=a_1x_1+a_2x_2+a_3x_3+...+a_nx_n\\&\\&\text {y si es en }\mathbb R^m\\&\\&\text{son m líneas como la anterior}\\&\text{El único valor constante que puede valer es 0}\\&\\&f(x_1,x_2,x_3,...,x_n)=0\text { es lineal}\\&f(x_1,x_2,x_3,...,x_n)=k\neq 0\text{ no es lineal}\end{align}$$Resumiendo, es lineal si y solo si cada línea es una combinación lineal de las variables (suma de variables multiplicadas por una constante)
5. No es lineal, tiene un valor constante distinto de 0.
6. No es lineal, tiene términos al cuadrado
7. Es lineal, sigue las reglas que he expuesto.
8. Es lineal, sigue las reglas expuestas.
9. No es lineal, no sirve el producto de variables.
10. Es lineal, sigue las normas
12. Es lineal, sigue las normas.
Y eso es todo, saludos.
:
:
;)
Hola antonio jimenez!
Son muchos ejercicios, hacemos un par de esos por pregunta, para evitar que se colapse el editor de ecuaciones.
Una transformación es lineal si verifica que
1) f(u+v)=f(u)+f(v)
2) f(k u)=k f(u)
$$\begin{align}&1.- \\&Sean\\&u=(u_1,u_2)\\&v=(v_1,v_2)\\&u+v=(u_1+v_1,u_2+v_2)\\&\lambda u= (\lambda u_1, \lambda u_2)\\&\\&T(u+v)=(u_1+v_1,0)\\&T(u)+T(v)=(u_1,0)+(v_1,0)=(u_1+v_1,0)\\&luego\\&T(u+v)=T(u)+T(v)\\&\\&\\&T(\lambda u)=(\lambda u_1,0)= \lambda(u_1,0)=\lambda T (u)\\&Si \ es \ una \ T.L.\\&\\&2.-\\&T(u+v)=(1,u_2+v_2)\\&\\&T(u)+T(v)=(1,u_2)+(1,v_2)=(2,u_2+v_2) \neq T(u+v)\\&\\&No \ es \ T.L.\\&\\&3.-\\&sean\\&u=(u_1,u_2,u_3)\\&v=(v_1,v_2,v_3)\\&u+v=(u_1+v_1,u_2+v_2,u_3+v_3)\\&\lambda u=(\lambda u_1, \lambda u_2, \lambda u_3)\\&\\&T(u+v)=(u_1+v_1,u_2+v_2)\\&T(u)+T(v)=(u_1,u_2)+(v_1,v_2)=(u_1+v_1,u_2+v_2)\\&Si \ cumple\\&\\&T(\lambda u)=(\lambda u_1, \lambda u_2)=\lambda(u_1,u_2)= \lambda T(u)\\&Si \ es \ T.L.\\&\\&4.-\\&T(u+v)=(0,u_2+v_2)\\&\\&T(u)+T(v)=(0,u_2)+(0,v_2)=(0,u_2+v_2)\\&Si\\&\\&T(\lambda u)=(0,\lambda u_2)=\lambda(0, u_2)=\lambda T(u)\\&\\&Si\ es \ T.L.\end{align}$$Manda las otras en dos preguntas o espera que otros expertos contesten
Saludos
;)
;)
;)
Te falta votar esta!
;)