¿Cómo se desarrollan las funciones discontinuas y como puedo realizar su gráfica?
Me piden desarrollar y graficar una función discontinua y describir brevemente cómo es su comportamiento en la gráfica y analiza por qué es continua, justifica tu respuesta.
1 Respuesta
·
·
¡Hola Elizabeth!
Y como ejemplos claros de funciones discontinuas tenemos aquellos en que el denominador se hace cero, por ejemplo esta:
f(x) = 1 / (x^2 - 4x)
El denominador se hace 0 cuando
$$\begin{align}&x^2 - 4x= 0\\&\\&x(x-4) = 0\\&\\&x_1=0\\&\\&x_2=4\end{align}$$Damos unos cuantos valores como antes, pero fíjaté que para 0 y 4 no podremos darlos ya que no está definido el dividir por 0, lo que si sabemos es que el límite será infinito.
He dejado que el programa calcule los puntos por donde pasa la función, es algo que supongo que sabrás hacer tú.
Y la gráfica que queda es esta:
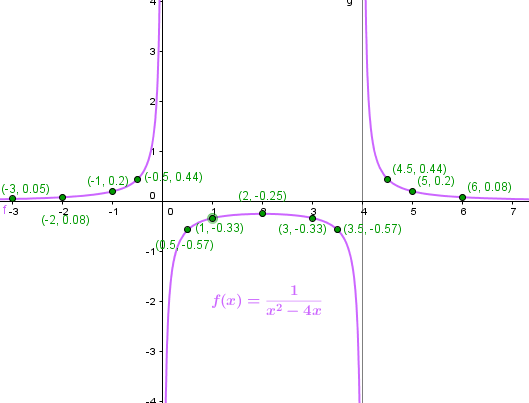
Esta función es discontinua en los puntos x=0 y x=4
La gráfica no se puede dibujar en un trazo, tienes que levantar el lapíz cuando pasas por el 0 y el 4. En estos valores el límite es infinito y la función no puede tomar ese valor. Además en cada punto un límite lateral es +infinito y el otro - infinito, otro añadido más para hacer que sea discontinua.
Y eso es todo, sa lu dos.
:
:
