Solución problema de álgebra: vectores
Alguien me podría dar la respuesta de este ejercicio por muchas veces que lo repita me da una solución diferente a la que me proporciona el libro.
·
·
¡Hola Scherezade!
Estas son las operaciones para calcular el rango:
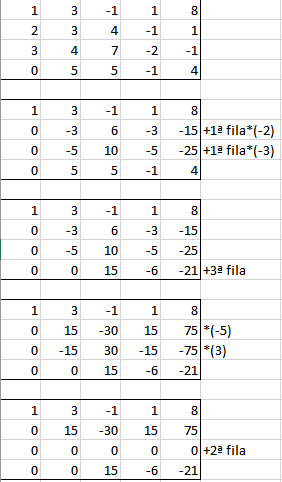
Y ya no se pueden hacer más ceros debajo de la diagonal, quedan tres filas linealmente independientes, el rango es 3.
b) Como base podríamos tomar esas tres filas, pero espera a ver si podemos mejorarlas un poco, por ejemplo está claro que la segunda fila se pude dividir por 15, y la tercera por 3, e intentaremos hacer algún cero por arriba si se puede.
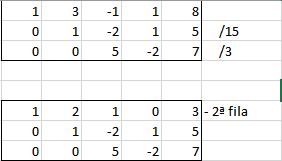
Luego la base es:
B={(1, 2, 1, 0, 3), (0, 1, -2, 1, 5), (0, 0, 5, -2, 7)}
·
(8, -4, 3, y4, y5) = a(1, 2, 1, 0, 3) + b(0, 1, -2, 1, 5) + c(0, 0, 5, -2, 7)
(8, -4, 3, y4, y5) = (a, 2a+b, a-2b+5c, b-2c, 3a+5b+7c)
Por igualdad vectorial se deducen estas igualdades escalares
a=8
2·8 +b = -4 ==> b=-20
8-2(-20)+5c = 3
48 +5c = 3
5c =-45
c = -9
Y ahora ya
y4 = b - 2c = -20 -2(-9) = -20 + 18 = 2
y5 = 3a+5b+7c = 3·8 +5(-20)+7(-9) = 24 -100 - 63 = -139
·
Y eso es todo, revisa las cuentas antes de presentarlo por si me he equivocado. Y no olvides valorar la respuesta con Excelente para poder recibir más respuestas.
Sa lu dos.
:
:
