¿Puede ser un vector propio (0,0,0)? Álgebra uned
Estoy resolviendo este ejercicio y calculando me aparece un autovector (0,0,0) creía que esto no era posible o no era válido
Gracias de antemano
1 Respuesta
·
·
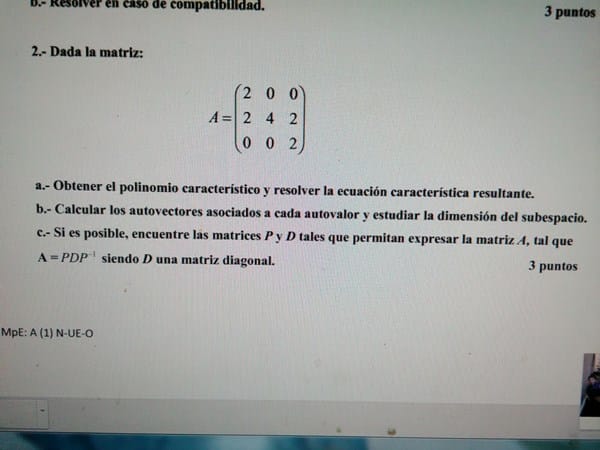
No, en la definición de vector propio se incluye que no sea nulo, el vector nulo siempre cumple
A·v = lambda · v
Para cualquier valor de lambda, pero lo que se busca son vectores no nulos.
·
¡POR FAVOR!
Si el polinomio característico es
(2-t)(4-t)(2-t)
no tienes que hacer tantas cuentas, ya tienes las raíces casi calculadas
lambda1 = 2
lambda2 = 4
lambda3 = 2
Para lambda = 2 te queda el sistema
2 2 2 | 0
Las soluciones son
(x, y, -x-y)
Y tomas dos vectores propios independientes
v_1= (1, 0, -1)
v_2 = (0, 1, -1)
Y para lambda= 4 te queda el sistema
-2 0 0
2 0 2
0 0 -2
Te queda x=0, z=0
Pero y puede tomar cualquier valor y le tienes que dar un valor distinto de 0, con lo cual el tercer vector propio es
v_3 = (0, 1, 0)
Y eso es todo, saludos.
:
:
