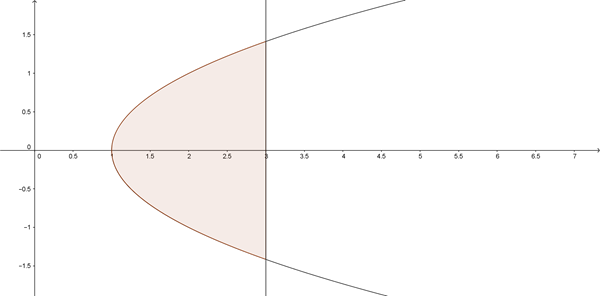Encuentre el volumen de un solido generado por rotar la región acotada
entre la parabola x = y² + 1 y la recta x=3 sobre la recta x=3
1 Respuesta
Respuesta de Lucas m
1
;)
Hola omar!
La superficie que gira es:
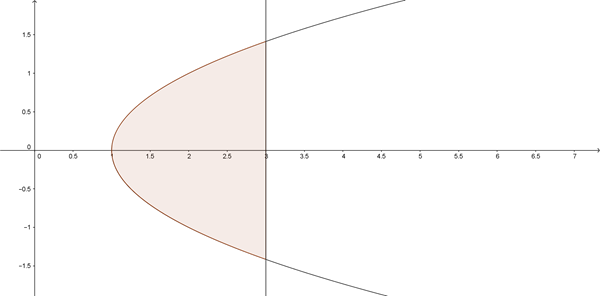
Calcularé, por el método de los discos o arandelas el volumen que genera la prte superior.
Por este método el diferencial es horizontal, perpendicular al eje de giro
El volumen se calcula con la integral:
V
$$\begin{align}&V= \pi \int_{y_1}^{y_2} \Big [R_g(y) \Big]^2dy\\&\\&R_g=radio\ de \ giro=desde \la \ función \ a \ x=3\\&\\&R_g=3-x=3-(y^2+1)=2-y^2\\&\\&y_1=0\\&\\&y_2:punto \ corte \ x=3 \ con \ la \ función\\&\\&y^2=x-1=3-1= \sqrt 2\\&y_2=\sqrt 2\\&\\&V= \pi \int_0^{\sqrt 2} \Big[2-y^2 \Big]^2 dy= \pi \int_0^{\sqrt 2} \Big(4-4y^2+y^4 \Big)dy=\\&\\&\pi \Big[4y-4 \frac{y^3}{3}+ \frac{y^5}{5} \Bigg]_0^{\sqrt 2}= \pi \Bigg(4 \sqrt 2- \frac{4}{3}2 \sqrt 2+ \frac{1}{5} 4 \sqrt 2\Bigg)\\&\\&=\frac{32}{15} \pi \sqrt 2\\&\\& V_T= \frac{64}{15} \pi \sqrt 2 \simeq18.9563 \ \ u^3\end{align}$$
