En métodos numéricos me plantean el siguiente problema donde debo:

·

·

¡Hola Sergio Davíd!

$$\begin{align}&c_k=\frac{f(b_k)a_k-f(a_k)·b_k}{f(b_k)-f(a_k)}\\&\\&\text{Si }c_k\text{es suficientemente pequeño ya está}\\&\\&\text{Si no, se toma como nuevos extremos } c_k \text{ y el valor }\\&a_k\; o\; b_k \text{ que tenga signo opuesto a }c_k\\&\text{Según sea eso puede darse}\\&[a_{k+1},b_{k+1}]=[a_k, c_k]\\&o\\&[a_{k+1},b_{k+1}]=[c_k,b_k]\\&\\&\text{Empezamos con }\\&a_1=0;b_1=1\\&\\&c_1= \frac{e^{-1}(3.2 sen1-0.5cos1)·0-e^0(3.2sen0-0.5cos0)·1}{e^{-1}(3.2 sen1-0.5cos1)-e^0(3.2sen0-0.5cos0)}=\\&\\&0.35939975\\&\\&Tenemos\\&f(a_1)=f(0)=-0.5\\&f(c_1)= f(0.35939975) =0.45894569\gt0.001\\&f(b_1)=f(1)=2.42255600\\&\\&\\&\text{Para que haya signos distintos de la función se debe tomar}\\&[a_2,b_2]=[0, \;0.35939975]\\&\\&c_2= \frac{e^{-0.35939975}(3.2 sen0.35939975-0.5cos0.35939975)·0-e^0(3.2sen0-0.5cos0)·1}{e^{-0.35939975}(3.2 sen0.35939975-0.5cos0.35939975)-e^0(3.2sen0-0.5cos0)}=\\&\\&0.18739317\\&\\&\\&Tenemos\\&f(a_2)=f(0)=-0.5\\&f(c_2)=f(0.18739317)=0.08698114\gt 0.001\\&f(b_2)=0.45894569\\&\\&\text{Para que haya signos distintos de la función se debe tomar}\\&[a_3,b_3]=[0, \;0.18739317]\\&\\&\end{align}$$

Y se siguen haciendo iteraciones tal como verás en la tabla de Excel

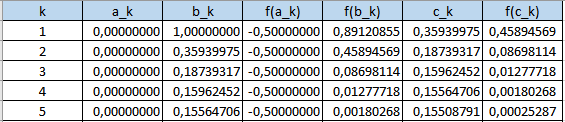
En la quinta iteración ya tenemos f(c_5) = 0.00025287 < 0.001, luego ya hemos encontrado la respuesta

x=0.15508791

Voy a comprobarla con Máxima:

Bueno parece que en el último decimal no coinciden, 0.00025287 contra 0.00025286 si redondeamos lo de Máxima, es un problema de precisión de Excel o de Máxima, pero está bien.

Te voy a dar la hoja de cálculo con este y otro ejercicio: Métodos numéricos para calcular raíces (dos).

Se podría mejorar la hoja con macros para que ella sola hiciera las cuentas necesarias hasta obtener un error menor, pero ya está bastante bien así, tu copias la ultima fila cuantas veces necesites abajo según la solución requiera más o menos iteraciones.

Sa lu dos.

:

: