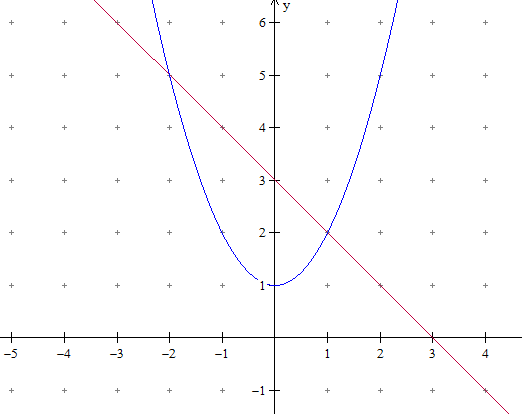La region acotada por la curva y = x^2 + 1 y la recta y=-x+3

;)
Superficie que genera el sólido:

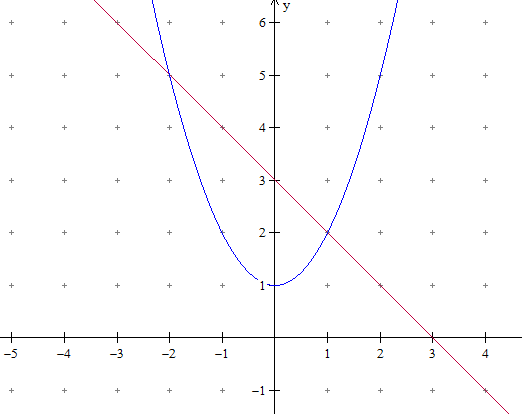
Primero calculas los puntos de corte, igualando las funciones:

x

$$\begin{align}&x^2+1=-x+3\\&\\&x^2+x-2=0\\&\\&x_1=1\\&\\&x_2=-2\end{align}$$

Ese volumen se calcula con la integral:

$$\begin{align}&V= \pi \int_{-2}^1[f(x)]^2-[g(x)]^2 dx=\\&\\&\pi \int_{-2}^1(-x+3)^2-(x^2+1)^2 dx=\\&\\&\pi \int_{-2}^1(x^2-6x+9-x^4-2x^2-1)dx=\\&\\&\pi \int_{-2}^1(-x^4-x^2-6x+8)dx=\\&\\&\pi \Big( \frac{-x^5}{5}- \frac{x^3}{3}-3x^2+8x \Bigg |_{-2}^1=\\&\\&=operando····\\&=\frac{117 \pi}{5}\simeq 73.51327···  u^3\end{align}$$

Sólido:

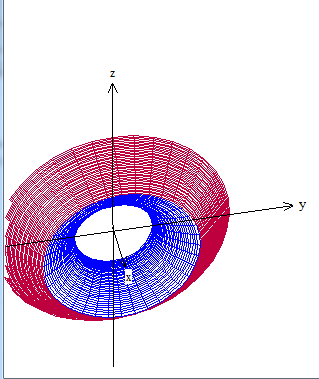
Saludos

;)

;)