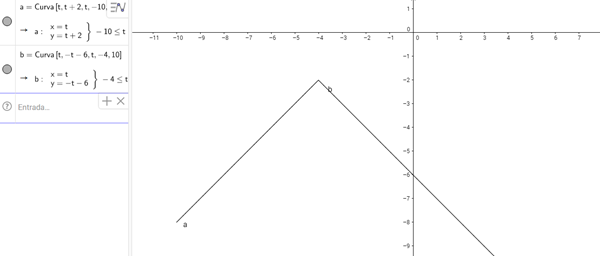
Como puedo saber si una función es diferenciable en x?
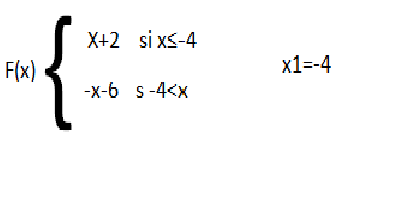
Calcule f´-(x1) y f´+(x1) y determine si f(x) es diferenciable en x1
Respuesta de Lucas m
1
2 respuestas más de otros expertos
Respuesta
1
Respuesta de Valero Angel Serrano Mercadal
1