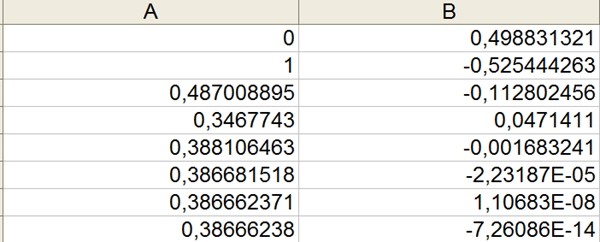
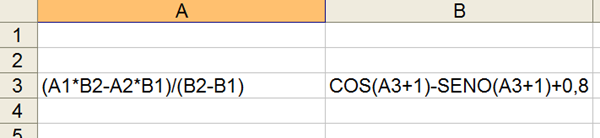
4. Obtener una raíz de la función f(x) = Cos (x+1) – Sen (x+1) + 0.8 en el intervalo [0,1] por el método de la secante. Entrar t
Este ejercicio es de métodos numéricos, del tema Error, Exactitud, Redondeo, Método del punto fijo, Método de Newton- Raphson, Método de la Secante, Método de la Regla falsa y Método de Bisección
Obtener una raíz de la función f(x) = Cos (x+1) – Sen (x+1) + 0.8 en el intervalo [0,1] por el método de la secante. Entrar también la quinta iteración resultante del proceso iterativo y dar los resultados con cuatro cifras decimales correctos.
2 Respuestas
;)
Hola henryvanegas!
f(0)=cos(0+1)-sen(0+1)+0.8=cos1-seb1+0.8= 0.498831321
Recuerda que la calculadora ha de estar en el modE radian.
Las siguientes iteraciones se calculan, según el método de la secante, con la fórmula:
$$\begin{align}&x_{n+1}=\frac{x_{n-1}·f(x_n)-x_n·f(x_{n-1})}{f(x_n)-f(x_{n-1})}\\&\\&\\&\\&x_0=0\\&x_1=1\\&\\&Así \ para\\&n=1\\&x_2=\frac{x_0f(x_1)-x_1f(x_0)}{f(x_1)-f(x_0)}=0.487008895 \Rightarrow f(x_2)=-0.11282456\\&\\&x_3=\frac{x_1f(x_2)-x_2f(x_1)}{f(x_2)-f(x_1)}\end{align}$$construyendo un Excel:
Solución: 0.3866 tiene cuatro decimales correctos
Las fórmulas de las celdas A3 y B3, que tienes que copiar en el rango inferior:
Saludos
;)
;)
;)
f(1)= cos(2)-sen(2)+0.8=-0,525444263
;)
