Usar el Método de Punto Fijo para aproximar la raíz de f(𝑥)=𝑥2+4𝑥−𝑒𝑥, comenzando con xo=0, con 5 iteraciones.

$$\begin{align}&f(x) = x^2 + 4x - e^x\\&\text{Sabes que el algoritmo plantea}\\&f(x) = x - g(x)\\&\text{Por lo que f(x) = 0, implica x = g(x)}\\&\text{Ahora el tema está en expresar la función que te dieron como 'x - g(x)'}\\&\text{Hay muchas formas y de la que elijas, dependerá la velocidad de convergencia de la solución}\\&\text{Voy a despejar una}\\&0 = x^2 + 4x - e^x = x(x+4) - e^x\\&x(x+4) = e^x\\&x = \frac{e^x}{x+4}\\&\text{Y ya tenemos nuestra función g(x) = }\frac{e^x}{x+4}\end{align}$$

Supongo que la expresión es:

Las iteraciones las voy a hacer con una pequeña tabla en Excel

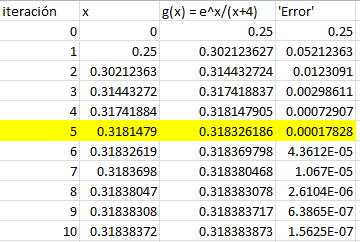
Te dice en 5 iteraciones por lo que deberías tomar el valor que pinté de amarillo, aunque claramente mejora tomando un par de iteraciones adicionales.

Salu2