Expresa el dominio y el condominio en forma de intervalo matemático y gráfico. F(x) = (3x^2) - 5x g(x) = (3-x) / (x^2-4)

·

·

¡Hola Ume!

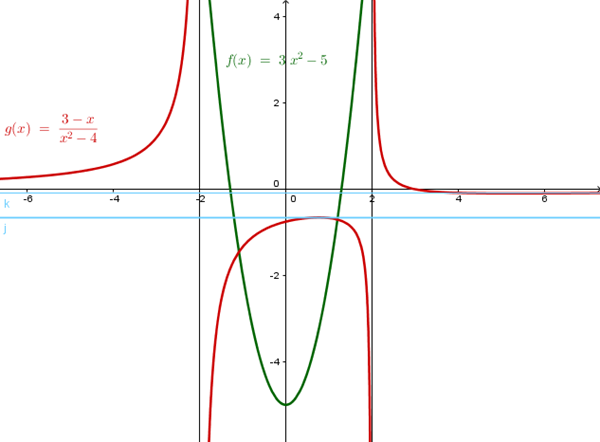
f(x) = 3x^2 - 5

Es un polinomio, los polinomios están definidos en todos los puntos R, por lo tanto

Dom f = R

o si se empeñan que sea en forma de intervalo pon

Dom f = (-infinito, +infinito)

El codominio es el dominio de la función inversa, para ello despejaremos x

$$\begin{align}&y = 3x^2 -5\\&\\&3x^2= y+5\\&\\&x^2= \frac{y+5}{3}\\&\\&x= \pm \sqrt{\frac{y+5}{3}}\\&\\&\text{para estar definida x debe ser}\\&\\&\frac {y+5}{3}\ge 0\\&\\&y+5 \ge0\\&\\&y \ge -5\\&\\&Rango f = [-5, +\infty)\\&\\&\\&2)  \\&\\&g(x) = \frac{3-x}{x^2-4}\\&\\&\text{Está definida en todo R salvo las raíces del denominador}\\&\\&x^2-4=0\\&\\&x^2=4\\&\\&x=\pm \sqrt 4 = \pm 2\\&\\&Dom\,f= \mathbb R-\{-2, 2\}\\&\\&\text{o en forma de intervalo}\\&\\&Dom\,f = (-\infty,-2)\cup(-2,2)\cup(2,+\infty)\\&\\&\text{Y el codominio (o rango) lo calculamos despejando x}\\&\\&y= \frac{3-x}{x^2-4}\\&\\&(x^2-4)y = 3-x\\&\\&x^2y-4y=3-x\\&\\&x^2y+x -4y-3=0\\&\\&Si \;y=0\implies x=3 \quad \text{0 pertenece al codominio}\\&\\&Si \;y\neq 0\\&\\&x= \frac{-1\pm \sqrt{1+4y(4y+3)}}{2y}\\&\\&\text{x estará definida si } \quad 1+4y(4y+3)\ge0\\&\\&16y^2 +12y+1 \ge0\\&\\&y=\frac{-12\pm \sqrt{144-64}}{32}=\frac{-3\pm \sqrt 5}{8}\\&\\&\text{la parábola es mayor que 0 a los extremos de las raíces}\\&\text{y entre ellas es menor que 0}\\&\\&Rango\,f = \left(-\infty,\frac{-3- \sqrt 5}{8}\right)\cup  \left(\frac{-3+\sqrt 5}{8},+\infty\right)\end{align}$$

El gráfico del dominio o codominio lo puedes hacer tú si es eso lo que piden, es sencillo una vez se han hecho los cálculos y carece de interés.  Mas importante son las gráficas de las funciones para comprobar si los codominios están bien calculados.

·
Y eso es todo, sa lu dos.

:

: