Para la función dada determine la solución real del respectivo dominio y rango
Para la función dada determine la solución real del respectivo dominio y rango
Me podrían ayudar con este ejercicio.
Respuesta de Lucas m
1
;)
Hola Jhon Fredy!
dominio:esa función se puede calcular siempre y cuando x-4>0 ===> x > 4
Dom f(x)= (4,+infinito)
El rango es el dominio de la función inversa.
Buscamos la inversa intercambiando las variables x e y.
$$\begin{align}&x=\frac{y-7}{\sqrt{y-4}}\\&\\&x \sqrt{y-4}=y-7\\&\\&elevando \ al \ cuadrado:\\&\\&x^2(y-4)=y^2-14y+49\\&\\&0=y^2-y(14+x^2)+(49+4x^2)\\&\\&Que \ se \ podrá \ calcular \ cuando \ el \ discriminante \ sea \ positivo:\\&\Delta=b^2-4ac \geq0\\&(14+x^2)^2-4(49+4x^2)\geq0\\&\\&196+28x^2+x^4-196-16x^2 \geq0\\&\\&x^4+12x^2 \geq 0\\&\\&x^2(x^2+12) \geq0\\&que \ es \ positivo \ para \ todo \x\\&Rang f(x)=(- \infty,+ \infty)\end{align}$$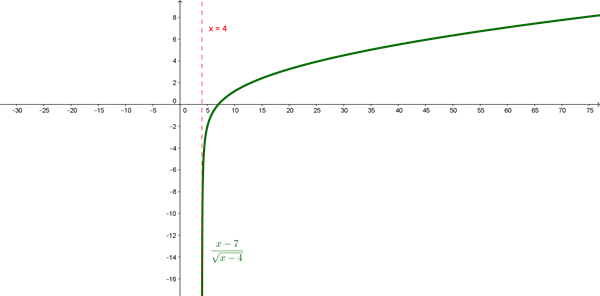
Saludos
;)
;)
