Situación y solución planteada: Un sistema vibratorio que consiste en una masa unida a un resorte como muestra la Fig:

Creo que antes habiamos visto el desarrollo de este problema.

Transcribo algunas partes:

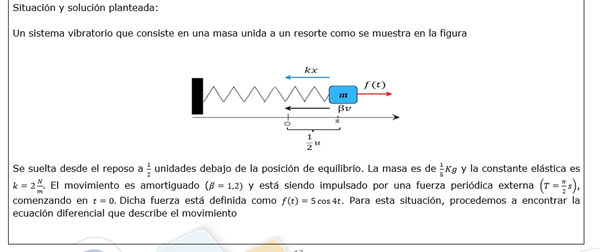
Espacio inicial= -0.5

masa = 1/5 Kg

K=2 N/m

Beta = 1.20

T= periodo de fuerza armonica exterior actuante= pi/2  seg.

Fext. = 5 cos 4 t

Partis de la Ley fundamental:  Fuerza = masa  x  aceleracion.

m (dx/dt)'' = -Kx - Beta (dx/dt)' + Fext. ......................

(dx/dt)'' +( K/m) x + Beta ((dx/dt)' = Fext.

( dx/dt)'' + (2/0.20) x + (1.2/0.20) ( dx/dt)' = (5/0.20) cos 4t

(dx/dt)'' + 10 x + 6 (dx/dt)' = 25 cos 4t................

Esta seria la ED para este movimiento.amortiguado y forzado.

La solucion de esta EcuaCION la estoy obteniendo de Wolfram-Alpha ya que el tema no lo manejo con soltura, y llegaria a:

La solucion general da de la forma:

x(t) = C1e^-3t sent  + C2 e^-3t cos t + 50/51 sen 4t - 25/102 cos 4t

Para los valores iniciales que te estan dando ....x(0) = -0.5  ...x'(0)=0 tendrias:

x(0) = C2 -( 25/102 )= -0.50 .........................C2=  - 0.50 + 25/102= -0.255

x'(0)= C1 + (50/51) x 4 = 0 ....................C1= - 3.92

Solucion = x(t) =  x(t) =( -3.92 e^-3t) sent  - (0.255 e^-3t) cos t + 50/51 sen 4t - 25/102 cos 4t.

Para la explicacion de solucion general de la ED invito al Profesor Valero quien dará la detallada forma de hallarla.