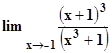Analicis de limites y continuidad, calculo diferencial
Quien me puede ayudar a resolver los limites de la imagen, y explicándome todo el proceso para poder comprenderlo mejor.

Respuesta de Lucas m
2
1 respuesta más de otro experto
Respuesta de Luis Alberto Candio Salcedo
2