Problema 4. Dadas las funciones f(x)=〖(x〗^2-x+2) y g(x)=(x+1). Determine analíticamente y compruebe con Geogebra

·

·

¡Hola Oscar!

Casi es más complicado verificar con Geogebra que hacerlo, pero vamos

a) f+g = (x^2-x+2) + (x+1) = x^2 + 3

b) g*f = (x^2-x+2)(x+1) = x^3 - x^2 + 2x + x^2 - x + 2 = x^3 + x + 2

c) Pienso que quieren decir composición

(f o g)(2) = f[g(2)]

g(2) = 2+1 = 3

f[g(2)] = f(3) = 3^2 - 3 + 2 = 9-3+2 = 8

ese es el resultado

d)  (g o f)(4) =g[f(4)]

f(4) = 4^2 - 4 + 2 = 16 - 4 + 2 = 14

g[f(4)] = g(14) = 14 + 1 = 15

·

Esto es lo que sale en Geogebra:

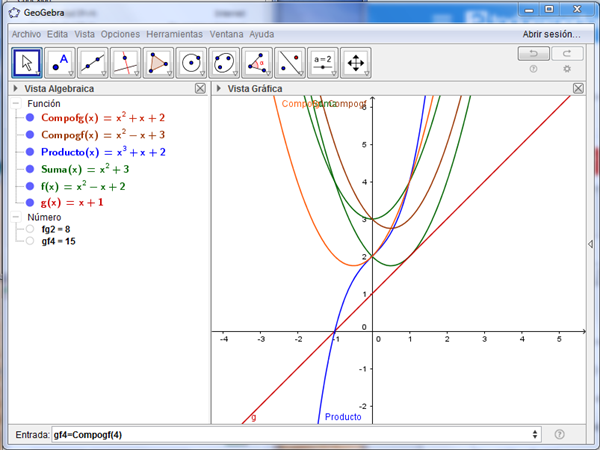
Pero lo más importante son las órdenes que se escribieron en la entrada, son estas:

f(x) = x^2-x+2

g(x) = x+1

Suma(x) = Simplifica[f(x)+g(x)]

Producto(x) = Simplifica[f(x)*g(x)]

Compofg(x) = Simplifica[f(g(x))]

Compogf(x) = Simplifica[g(f(x))]

fg2 = Compofg(2)

gf4 = Compogf(4)

·

Y eso es todo, saludos.

:

: