··
..
¡Hola Jorge!
No están usando un lenguaje propio de la lógica, se supone que quieren decir:
"Si el reloj marcaba las 8:00 de la noche, entonces Carlos salió de su trabajo a las 7:00 pm y vio salir a Jaime de la empresa. Si la información de Jaime es veraz, entonces Carlos no vio salir a Jaime de la Empresa. La información de Jaime es veraz o estaba en la empresa en el momento del robo del dinero. El reloj marcaba las 8:00 de la noche. Por lo tanto, Jaime estaba en la empresa en el momento del robo del dinero”
Lo único que he hecho es añadir un "Si" al principio para que ya sean todo proposiciones lógicas con todos sus conectores.
p = El reloj marcaba las 8:00 pm
q = Carlos salió de su trabajo a las 7:00 pm
r = Carlos vio salir a Jaime
s = La información de Jaime es veraz
t = Jaime estaba en la empreesa en el momento del robo del dinero
Las premisas son:
p --> (q^r)
s --> ~r
s v t
p
Y la conclusión es:
t
Lo hago primero por reglas de inferencia.
Si nos obligan a que t sea verdadero veamos las premisas donde aparece, solo lo hace en esta
s v t
Nos obligan a que sea verdadero porque sino sería falsa esa premisa, luego seguramente es que s es falsa.
Investigamos entonces otros lugares dode aparece s
s --> ~r
por modus tollens podemos poner
r--> ~s
Y r se cumplirá si se cumple p por modus ponens en la premisa primera.
Y ahora en vez de ir de la conclusión al principio vamos de las premisas a la conclusión
Como nos dicen que se cumple p se cumple (q^r), luego se cumple r, luego no se cumple s, luego es obligatorio que se cumpla t. El razonamiento está bien.
Yo quitaría la proposición q que no sirve para nada al salir solo una vez, pero ya lo hice otra vez y te obligaron a ponerla, así que la dejo.
Lo que hay que demostrar en la tabla de la verdad es:
{[p --> (q^r)] ^ (s --> ~r) ^( s v t) ^ p} --> t
Esta es la tabla de la verdad:
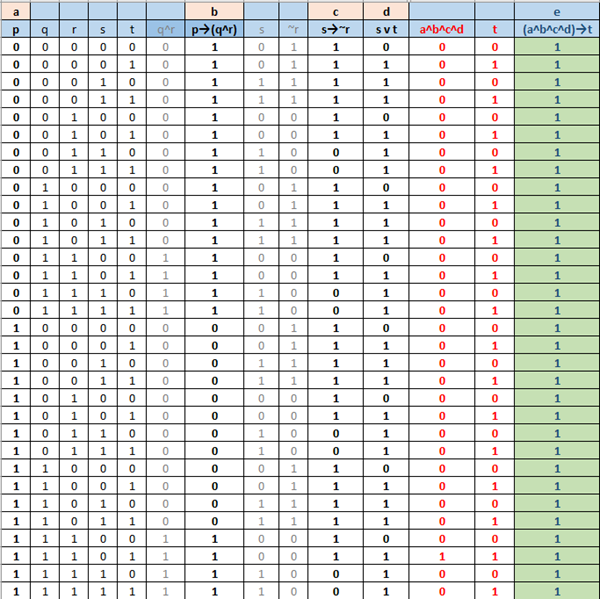
Como puede verse es una tautología.
Y para la tabla TRUTH hay que escribir:
{[p > (q&r)] & (s > ~r) & (s+t) & p} > t

Y eso es todo, s a l u d o s.
::
..


