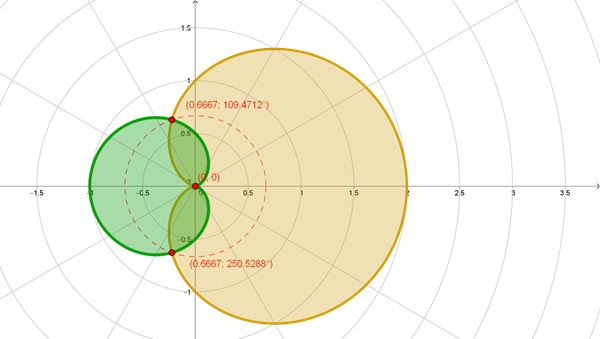
Hallar los puntos de intersección de las curvas
Es un problema de Geometría Analítica, donde me da las ecuaciones pero en coordenadas polares, ¿Pueden por favor ayudarme, ya que no la comprendo muy bien?
r=1+Cosθ y r= 1/2(1-Cosθ)
Respuesta de Lucas m
1
1 respuesta más de otro experto
Respuesta
1