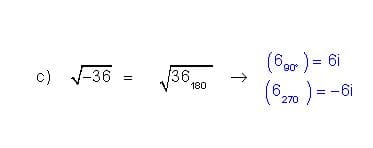Números complejos:no entiendo el cálculo del módulo

Yo creo que sí jajaja, lo has dicho bien la raíz de 1296 es 36 pero te piden la raíz cuadrada de 36 !, no de 1296, la raíz cuadrada de 36=6.

Si tienes dudas pregunta:)

Cómo puedes ver aquí, así es como calculo el módulo. Por qué el mío no está bien? Sigo empeñada en que el módulo es 36 y  no 6. Gracias.

Vale, estás mezclando 2 formulas diferentes.

Primero para hallar el módulo de un número complejo usas:

$$\begin{align}&M=\sqrt{a^2+b^2}\end{align}$$

Siendo a y b la parte real e imaginaria respectivamente. 

Por otro lado quieres calcular la raíz de un número complejo. Para ello haces la raíz del módulo y calculas el argumento con (2kpi/n con n=0,..., n-1; siendo n el orden de la raiz). Pero según tengo entendido la pregunta es con el módulo solamente.

Verás para hacer la raíz interesa tener el número complejo en forma polar( o módulo-argumento); por tanto primero calculas el módulo.

El -36 es lo mismo que el -36 + 0i, es decir no tiene parte imaginaria, estos número son los que tendrías que meter en la fórmula, a=-36 y b= 0

$$\begin{align}&M=\sqrt{(-36)^2+0^2}=\sqrt {36^2}=36\end{align}$$

Por tanto el módulo es 36, esto se puede ver directamente imaginandote el vector del número en el plano complejo , el -36 esta situado en la recta real en sentido negativo por tanto el argumento será 180º ( o -180º). 

Ahora si haces la raíz al número el resultado tendrá por módulo la raíz de del número ( 6) y el ángulo lo que tienes ahí.

Espero haberte aclarado un poco, te recomiendes que repases el concepto de forma polar y su representación en el plano complejo, esto facilitará mucho que entiendas estos resultados:)

Por lo que entiendo entonces, el módulo de -36 sería 36 pero como lo que estoy estudiando es el número raíz de -36, el módulo sería 6, es correcto?

;)

Hola teresa!

$$\begin{align}& \sqrt {36}_{180º}=6_{\frac {180º+k·360} {2}}\\&\\&k=0 ===> 6_{90º}=6i\\&\\&k=1 ===> 6_{275º}=-6i\end{align}$$

Saludos

;)

;)

Hola:

Gracias por atenderme. No entiendo de donde sale raíz de 36 180º. ¿Puedes explicármelo?

;)

El módulo de un complejo z=a+ bi , se calcula como 

$$\begin{align}&|z|= \sqrt{a^2+b^2}\\&luego\\&-36=-36+0i  \ \ es \ un \ número \ real\\&a=-36\\&b=0\\&|z|=\sqrt{(-6)^2+0^2}= \sqrt {36}=6\\&\\&argumento:\\&tan(\alpha)=\frac b a=\frac {0}{-36}=0\\&arctan(0)=0º \ o \ 180º\end{align}$$

como es un número negativo,se representa en el eje Real(X) negativo===> 180º

Las fórmulas que te he puesto arriba para calcular el módulo y el argumento son de carácter general. Pero hay 4 casos que no haría falta aplicarlas si tienes en cuenta que el módulo es la distáncia al Origen de coordenadas(distancia es siempre positiva) y el argumento el ángulo que forma el afijo(punto que representa el complejo) con el eje X positivo.

Esos 4 casos son cuando los complejos se encuentran sobre los ejes:

Por ejemplo:

z=5=5+0i    al ser un número real positivo se representa en las X positivas.Su módulo evidentemente será 5,ya que estáa 5 unidades del 0, y su argumento 0º.Los ángulos se empiezan a medir desde el eje X positivo y en sentido antihorario.

z=-5=-5+0i  .Es un número real negativo, se representa en el eje Real (X)negativas.

Su distancia al origen es 5. El módulo siempre es positivo, y el -5 está a 5 del origen. El eje X negativo respecto el X positivo, girando con centro el Origen de coordenadas, lo has de girar 180º. El argumento de todos los Reales Negativos es 180º

z=5i=0+5i Es un complejo llamado Imaginario puro(no tiene parte real). La parte imaginaria se representa en el eje Y. Su afijo sería el punto (0,5). Su módulo directamente es 5 y su argumento 90º. Del eje X positivo lY positivo en sentido antihorario has de girar 90º

z=-5i=0-5i Imaginario puro que se representa en el afijo (0,-5), punto que está en eleje Y negativoadistancia 5(módulo) del Origen de coordenadas y argumento 270º (has de girar tres rectos en sentido antihorario para pasar del X+ al Y-)

En todos los demás casos has de aplicar la fórmula del módulo y del argumento

Saludos

;)

;)