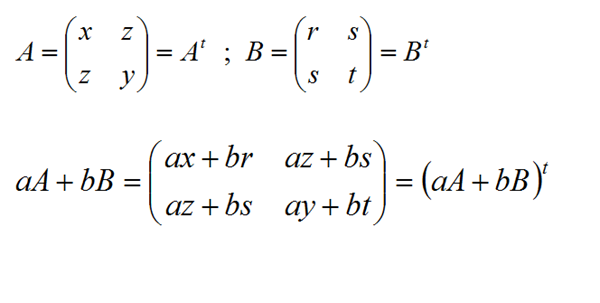Sea el conjunto N = {Matrices Simétricas Cuadradas N2x2} y sea V el espacio vectorial conformado por las matrices cuadradas M2x2

Demostrar que N es un subespacio del espacio vectorial V.

1 respuesta

Respuesta
1

;)
Hola Brayan!

Será un subespacio vectorial si para cualesquiera dos matrices cuadradas y simétricas, A y B se verifica aA+bB también son cuadradas y simétricas, siendo a y b escalares.

Una matriz es simétrica si es igual a su traspuesta; luego

Luego la combinación lineal es 2x2 y simétrica luego es subespacio vectorial

Saludos

;)

;)

Añade tu respuesta

Haz clic para o

Más respuestas relacionadas

Quien sabe cómo calcular el tiempo de vaciado de un tanque

Quien sabe cómo calcular en cuántas horas se vacía un tanque el cuál tiene una capacidad de 1200 litros sabiendo que cada 6,3 segundos el tanque baja 0,5 litros en cuántas horas o minuto el tanque queda vacío
2 respuestas

Ejercicio sobre Regla de tres

Una moto recorre una distancia en 3 horas a 60km/h ¿A qué velocidad debe ir para recorrer la misma distancia en 2horas? Yo hice el ejercicio así Horas Velocidad 3 60km/h 2 x x= 40 km/h No se si lo tenga bueno tengo una duda porque poniendole lógica...
2 respuestas

Cuantos kg de un producto me quedan en un cubo de capacidad de 1000 litros con un producto que tiene una densidad de 1.33 kg/l

Quien sabe cómo hacer el calculo para saber cuantos kg de un producto me quedan en un cubo de capacidad de 1000 litros en el cual hay un producto que tiene una densidad de 1.33 kg/l y solo me quedan en el cubo 29 cm de producto
1 respuesta

Ley de tercios en casinos

Me puedes ayudar por favor con este tema para ver como funciona matemáticamente.
12 respuestas

Desarrollar un problema matemático: Una familia va de vacaciones diez días. Se alojan en un hotel con pensión completa, el coste

Una familia va de vacaciones diez días. Se alojan en un hotel con pensión completa, el coste del cual representa 3/5 de su presupuesto, gastándose 2/3 del resto en ocio. Si vuelven a casa con 640€, ¿Cuál era su presupuesto para las vacaciones?
1 respuesta

Calcular el límite de nx^n sin usar L'Hôpital

Se que la sucesión x^n converge a 0 cuando |x|<1. Y como x^n tiende a cero más rápido de lo que n crece, la intuición me dice que nx^n debe converger a cero cuando |x| < 1. Pero no sé cómo demostrarlo sin usar la regla de L' Hôpital. ¿Me pueden dar...
1 respuesta

Demostrar que f(x) = x + sen(x) es creciente

Nos piden hacer la demostración, sin usar el criterio de la derivada (que si es positiva en un intervalo, entonces f es creciente), sólo usando la definición. Hay que demostrar que si x < y, entonces x + sen(x) < y + sen(y) Lo que se es que -x <...
1 respuesta

Problema de ecuaciones

En un almacén, el número de botellas que contiene cada caja excede en 3 al número de cajas. Si hay un total de 270 botellas, ¿Cuántas cajas hay en el almacén?
2 respuestas

Si l(x) = mx+b corta la gráfica de f(x) = x^2 en un punto único, entonces l(x) es la recta tangente a f en el punto de corte

Hay que demostrar lo que dice el enunciado. Suponiendo que (a, a^2) es el punto de corte y es único, debemos llegar a que m = 2a y b = -a^2 Porque la recta tangente está dada por T(x) = 2a(x - a) + a^2 = 2ax - a^2. Además, f(a) = l(a) = T(a) a^2 = ma...
2 respuestas

Te invito a ganhar la Quiniela en Buenos Aires Argentina, com 4 cifras Millar;,siganas pagas lamitad https://notitimba2

You can set up Google Alerts to receive emails when your chosen keywords appear in new online content, such as news articles, blogs, or web pages. Te invito a ganhar la Quiniela en Buenos Aires Argentina, com 4 cifras Millar;, siganas pagas lamitad...
Sin respuestas