Anónimo
Resolver ejercicio de lógica proposicional de acuerdo a los requerimientos
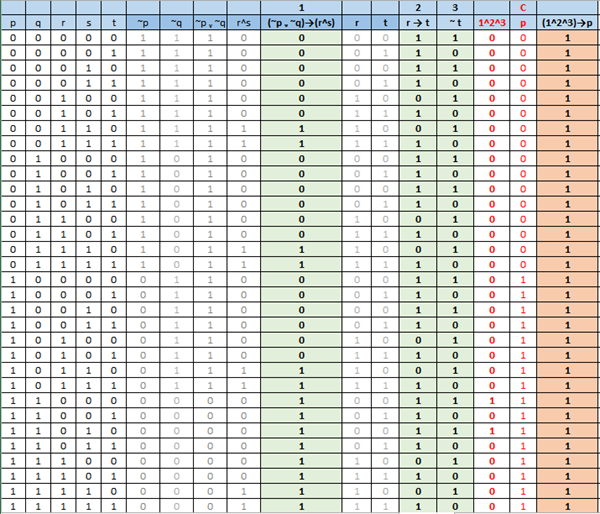
Identificar (del texto dado), los razonamientos lógicos inductivos y deductivos, y en ellos el tipo de razonamiento. A partir de los razonamientos propuestos para el texto, responder la pregunta: ¿Se verifica la conclusión propuesta? Y presentar argumentos que permitan respaldar veracidad a la respuesta dada. Es decir, a partir de las tablas de verdad y las leyes de inferencia demostrar la validez o no del razonamiento. Además adjuntar pantallazo del uso del simulador de Tablas de Verdad.
. Si el Rector no pudo dar el discurso o los diplomas no llegasen a tiempo, entonces la fiesta de graduación tendría que cancelarse y los estudiantes se enojarían. Si la fiesta se cancelara, habría que devolver el dinero. No se devolvió el dinero. Por lo tanto, el Rector pudo dar el discurso
1 respuesta
·
·
¡Hola David!
Las proposiciones simples y compuestas eran estas:
Las proposiciones simples son:
p = el rector no pudo dar el discurso
q = los diploman llegan a tiempo
r = cancelar la fiesta de graduación
s = enojarse los alumnos
t = devolver el dinero
Y las proposiciones compuestas son
1) (~p v ~q) --> (r ^ s)
2) r --> t
3) ~t
C) p
Es verdadero porque aplicando modus tollens en 2) y 3) tenemos que se cumple
~r
Luego r es falso
Luego r^s es falso
Luego ~p v ~q debe ser falso, ya que si fuese verdadero 1) sería falso
Luego ~p debe ser falso
Luego p debe ser verdadero.
·
Lo que hay que demostrar en la tabla de la verdad es esta proposición
{[(~p v ~q) --> (r ^ s)] ^ (r --> t) ^ (~t)} --> p
Y esta es la tabla, algo complicada.
Y sale todo unos (verdaderos) en la ultima columna, luego es una tautología, el razonamiento ha sido correcto.
·
Y con Truth Table lo que hay que introducir es:
{[(~p + ~q) > (r & s)] & (r > t) & (~t)} > p
Y eso es todo.
Sa lu dos.
:
: