Dimensiones de un cono de menor volumen

;)
Hola andrea!

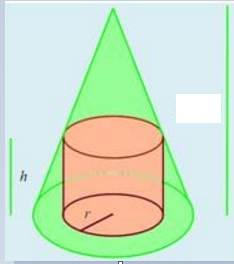
En este dibujo los datos son R y H del cilindro

Variables r y h del CONO

Sean S vértice cono

Q centro círculo superior del cilindro

O el centro de los círculos de las bases.

QN =R  ; OQ=H

OA=r ; ; OS =h

Volumen del cono V= 1/3 pi r^2 h^3

Hemos de relacionar el radio r y altura h del cono:

Sección axial:

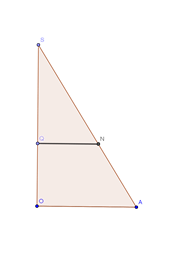
semejanza de triángulos SQN y SOA:

$$\begin{align}&\frac{SQ}{SO}=\frac{QN}{OA}\\&\\&\frac{h-H} h= \frac R r ===> r=\frac{hR}{h-H}\\&\\&V_{con}= \frac13  \pi r^2h= f(r,h)\\&\\&V(h)= \frac 1 3 \pi \Big(\frac{hR}{h-H} \Big)^2·h= \frac{\pi R^2}3· \frac{h^3}{(h-H)^2}\\&\\&V'(h)=\frac{\pi R^2}3 · \frac{3 h^2(h-H)^2-2(h-H)h^3}{(h-H)^4}=simplificando=\\&\\&\frac{\pi R^2}3 \frac{3h^2(h-H)-2h^3}{(h-H)^3}=\\&\\&\frac{\pi R^2}3·\frac{h^3-3h^2H}{(h-H)^3}===> V'(h)=0\\&\\&\\&\frac{\pi R^2}3·\frac{h^3-3h^2H}{(h-H)^3}=0===>  h^3-3h^2H=0 ==>\\&\\&h^2(h-3H)=0   \\&\\&h-3H=0\\&\\&h= 3H\\&\\&r= \frac {hR}{h-H}=\frac{3HR}{2H}=\frac 3 2 R\\&\\&Comprobación \ mínimo (criterio \derivada \ primera)\\&V'(h=2H)= \frac 1 3 \pi R^2  \frac{(2H)^3-3(2H)^2H}{(2H-H)^3}=  \frac{8H^3-12H^3}{H^3}<0 ==> decreciente \ a\ la \ izquierda\\&\\&V'(h=4H)= \frac 1 3 \pi R^2  \frac{(4H)^3-3(4H)^2H}{(2H-H)^3}=  \frac{64H^3-48H^3}{H^3}>0==> \ creciente \ a\ la \ derecha\end{align}$$

Luego es un mínimo  para una altura del cono triple de la del cilindro h=3H

y radio 1.5 veces      r= 3/2R

Saludos y recuerda que has de votar la respuesta

;)

;)

;)
En los temas además de cálculo pon matemáticas (si no puedo no verlo)y profesores, univerdidades::::

;)