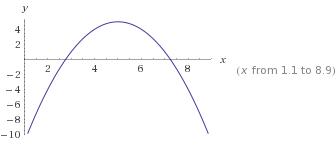
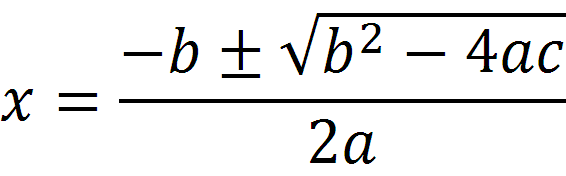Buen Día a) Una bala se dispara desde el piso formando una trayectoria tipo parábola, donde su ecuación es: y = -x2 + 10x – 20
a) Una bala se dispara desde el piso formando una trayectoria tipo parábola, donde su ecuación es: y = -x2 + 10x – 20.
Resuelve:
¿En qué punto, la bala, alcanzó su altura máxima?
Determina los puntos desde donde fue lanzada la bala, así como el punto en donde cayó.
Teniendo la trayectoria es fácil calcular lo que te están pidiendo:
y = -x2 + 10x – 20.
Al alcanzar la altura máxima su velocidad vale 0. Esta detenida allí. Luego puedes hacer:
y' = dy/dt = -2x+10 ........y la anulas...con lo cual x= 5 metros del lanzamiento.
Para la segunda cuestión debes igualar la ecuación de la trayectoria a 0. ( porque te dicen que se lanza desde el nivel del piso)...
0 = -x2 + 10x – 20......que tiene por raices: x1= 2.764 y x2= 7.236 que serian respectivamente coordenada de lanzamiento y coordenada de llegada.
Anónimo novato... recuerda que las respuestas que te son útiles debes calificarlas. Es nuestro única motivación para seguir ayudandolos.
1 respuesta más de otro experto
Como se trata de una parábola, y ya te da la ecuación, para mayor comodidad pasamos del otro lado el -x^2 + 10x -20 y quedaría la ecuación de la parábola como:
$$\begin{align}&x^2-10x+y+20=0\end{align}$$Una vez teniendo la ecuación general de la parábola, pasamos la ecuación en su forma ordinaria, quedando de tal manera:
$$\begin{align}&(x-5)^2=-1(y-5)\end{align}$$la ecuación ordinaria nos da el vértice la curva, el cual es el punto mas alto de la parábola por lo tanto el punto mas alto o el vértice es (5,5).
Ahora para encontrar desde donde salio y cayo la bala, podemos encontrar tomar la ecuación inicial y = -x^2 + 10x – 20 y llevarla a la fórmula general teniendo en cuenta lo siguiente
a=-1
b=10
c=-20
Sustituyendo los valores de la fórmula general te dará dos valores
X1= 2.76 y x2= 7.23, el cual x1 seria el punto donde salio la bala y x2 en donde vayo la bala.