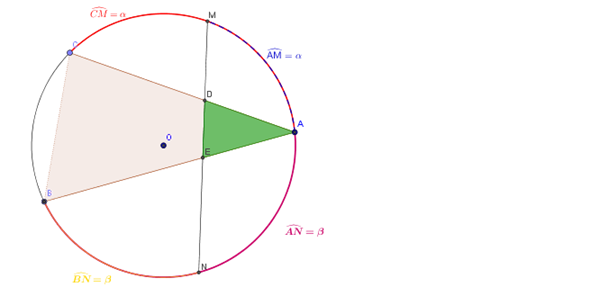
Se da un ángulo inscrito BAC, en una circunferencia, MN trazo que une los puntos medios de los arcos subtendidos ...
... Por cada uno de los lados de ángulo, corta dichos lados en D y E respectivamente. Demuestre que el triangulo DEA es isósceles.
1 respuesta
Respuesta de Lucas m
1
;)
Hola Blanca!
Entiendo lo siguiente:
Los arcos CM y MA son iguales y valen alfa.(Recuerda que lamedida angular de un arco me la da su ángulo central(COM=MOA)
Los arcos BN y NA son iguales y valen Beta.
Son iguales por ser M yN lospuntos medios del arco
Los ángulos CDM=NDA son interiores y por tanto iguales a la semisuma de los arcos que abarcan:
$$\begin{align}&anguloCDM=\frac{ \alpha + \beta} 2\end{align}$$Por la misma razón angulo MEA=BEN (opuestos por el vértice) y valen tambien la semisumade losarcos que abarcan por ser E interior:
$$\begin{align}&anguloMEA=\frac{ \alpha + \beta} 2\end{align}$$Luego en D y en E el triaángulo AED tiene los mismos ángulos y por tanto es isósceles
Saludos
Y recuerda votar
;)
;)
