Se considera la curva definida por f(x)=x^3/(x^2+1)
Se pide:
1. Demostrar, sin calcular, que existe un punto donde la función corta al eje OX.
2. Intervalos de monotonía de la función. ¿Tiene extremos relativos la función?
3. Intervalos de concavidad y conver¡Xidad y puntos de inflexión
4. Realiza el esquema de la grafica de la curva f(x)=(x^3/(x^2+1))+1
1 Respuesta
;)
Hola Miriam!
Te contesto desde el móvil. No puedo abrir el editor de ecuaciones ni adjuntar imágenes. Así que no lo puedo hacer todo detallado.
1. Esa función es continua en todo R
x^2+1=0. ==>x^2=-1 sin solución
==> Dominio f=R
Observa también que el denominador es siempre positivo, y el numerador es positivo para x>0; y negativo para x<0. Aplicando el Teorema de Bolzano esa función al menos corta una vez al eje X.
Para calcularlo y=0. ==> x^3=0 ==> x=0
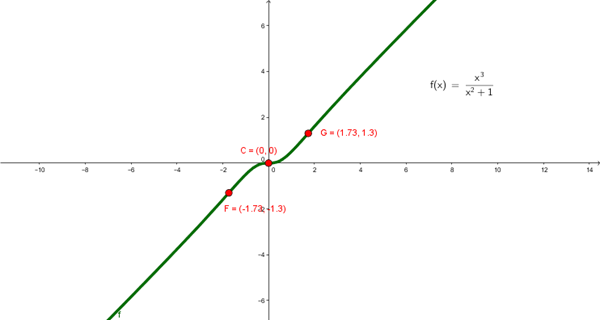
Pasa por el origen de coordenadas (0,0)
2.
Y'=(x^4+3x^2)/(x^2+1)^2
Y'=0
x^4+3x^2=0
x^2(x^2+3)=0. ===> x=0
Intervalos crecimiento:
(-infinit,0) y'(-10) >0
(0,+infinito) y'(10) >0
La función es creciente siempre.
X=0 es un punto de inflexión con tangente horizontal. No tiene extremos relativos
3)
Y''=(-2x^3+6x)/(x^2+1)^3
Y''=0. ===>. -2x^3+6x=0
X(-2x^2+6)=0
X=0. X= sqrt(3). X=-sqrt (3)
Tiene tres puntos de inflexión.
Intervalos concavidad:
(-Infinit,-sqrt3) y''(-10)>0. Cóncava hacia arriba
(- Sqrt 3,0) y''(-1)<0 convexa hacia abajo
(0, sqrt 3) y''(1)>0 cóncava
(Sqrt 3,+infinito) y''(10)<0 convexa
La gráfica te la adjunto el Lunes
¿Podría poner el proceso de calculo de la segunda derivada? No me sale lo mismo.
Gracias
;)
Y''=[(4x^3+6x)(x^2+1)^2-(x^4+3x^2)2(x^2+1)2x]/[(x^2+1)^4]
Simplificando un (x^2+1) en cada sumando
=
[(4x^3+6x)(x^2+1)-4x(x^4+3x^2)]/[(x^2+1)^3]
=
(4x^5+4x^3+6x^3+6x-4x^5-12x^3)/(x^2+1)^3
(-2x^3+6x)/(x^2+1)^3
;)
¡Gracias!
¿Para definir los intervalos del dominio y de curvatura porque a veces se usa paréntesis y otras corchetes si esos puntos están comprendidos en el dominio?
Perdón, me refiero a los intervalos de curvatura y monotonía
Siempre se usan paréntesis
Ya que por ejemplo en los de crecimiento
(-infinit,0) y'(-10) >0
(0,+infinito) y'(10) >0
x=0 es donde cambia el crecimiento y por ser un punto crítico y'(0)=0 y en ese punto ni crece ni decrece por eso no se incluye en el intervalo
En la concavidad pasa lo mismo:
(-Infinit,-sqrt3) y''(-10)>0. Cóncava hacia arriba
(- Sqrt 3,0) y''(-1)<0 convexa hacia abajo
(0, sqrt 3) y''(1)>0 cóncava
(Sqrt 3,+infinito) y''(10)<0 convexa
En x=0 i x=sqrt 3 i x=-sqrt 3 la y''=0 son los puntos de inflexión i allí la función no es ni cóncava ni convexa por eso se pone (intervalo abierto)
;)
;)
Gráfica:
F,C i G puntos Inflexión
;)
