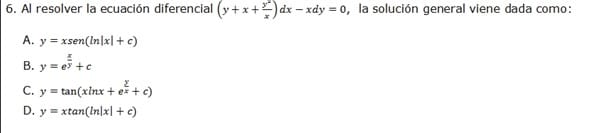Quien me desarrollo un problema de ecuaciones matemáticas
Gracias estimado experto por la colaboración en este problema de ecuaciones
Respuesta de Lucas m
3
$$\begin{align}&\\&p\\&\end{align}$$;)
Hola Andres Palomino!
Buscaremos la separación de variables con la sustitución:
$$\begin{align}&u= \frac y x \\&\\&(y+x+ \frac{y^2} x)dx=xdy\\&\\&\Big( \frac y x+1+ \frac{y^2}{x^2}\Big)dx=dy\\&\\&\frac{dy}{dx}=\Big( \frac y x+1+ \frac{y^2}{x^2}\Big)\\&\\&y=ux==> \frac{dy}{dx}=\frac{du}{dx}x+u\\&\\&x \frac{du}{dx}+u=u+1+u^2\\&\\&x \frac{du}{dx}=1+u^2\\&\\&\frac{du}{1+u^2}= \frac{dx} x\\&\\&\int \frac{du}{1+u^2}= \int \frac{dx} x\\&\\&arctanu=ln|x|+C\\&\\&u=tan \Big(ln|x|+C\Big)\\&\\& \frac y x= tan \Big(ln|x|+C\Big)\\&\\&y=xtan \Big(ln|x|+C\Big)\\&\end{align}$$La D
Saludos
;)
;)
