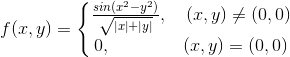Cómo probar si la función es continua en varias variables?
Me dan una función y me piden que debo probar si es continua o no. Sé que lo primero es ver si la función existe o no. Por tanto, selecciono trayectorias y luego pruebo con el teorema del emparedado. Se supone que la función existe, lo que no sé es como probarlo con el teorema del emparedado.
Respuesta de Lucas m
1
;)
Hola Daniel!
Utilizando infinitésimos equivalentes :
$$\begin{align}&\lim_{(x,y) \to (0,0)}\sin(x^2-y^2)= \lim_{(x,y) \to (0,0)}(x^2-y^2)\\&\\&límites \ reiterados:\\&\lim_{(x,y) \to (0,0)}\frac{\sin(x^2-y^2)}{ \sqrt {|x|+|y|}}= \lim_{(x,y) \to (0,0)}\frac{(x^2-y^2)}{ \sqrt {|x|+|y|}}=\\&\\&\lim_{x \to 0}\Bigg(\lim_{y\to 0} \frac{(x^2-y^2)}{ \sqrt {|x|+|y|}}\Bigg)=\lim_{x \to 0} \frac{x^2}{ \sqrt {|x|}}=\lim_{x \to 0} |x|^\frac 3 2=0\\&\\&\\&\lim_{y \to 0}\Bigg(\lim_{x\to 0} \frac{(x^2-y^2)}{ \sqrt {|x|+|y|}}\Bigg)=\lim_{y \to 0} \frac{-y^2}{ \sqrt {|y|}}=-\lim_{y \to 0} |y|^\frac 3 2=0\\&\\&Límites \ Radiales\\&y=mx\\&\lim_{(x,y) \to (0,0)}\frac{(x^2-y^2)}{ \sqrt {|x|+|y|}}=\lim_{x \to 0}\frac{(x^2-m^2x^2)}{ \sqrt {|x|+|mx|}}=\\&\\&\lim_{x \to 0}\frac{|x|^\frac 3 2(1-m^2)}{ \sqrt {1+|m|}}=0\\&\\&No \ dependen \ de \ m\\&\\&En \ polares:\lim_{(x,y) \to (0,0)}\frac{(x^2-y^2)}{ \sqrt {|x|+|y|}}\\&\\&\lim_{ r \to 0}\frac{r^2cos^2 \theta-r^2sen^2 \theta}{\sqrt{|r \cos \theta|+| r sen \theta|}}=\lim_{ r \to 0}\frac{r^2(\cos^2 \theta-sen^2 \theta)}{\sqrt{|r \cos \theta|+| r sen \theta|}}=\\&\\&\lim_{ r \to 0}\frac{r^2cos(2 \theta)}{\sqrt{|r \cos \theta|+| r sen \theta|}}=\\&\\&\lim_{ r \to 0}\frac{|r|^\frac 32cos(2 \theta)}{\sqrt{| \cos \theta|+| sen \theta|}}=0\\&\\&No \ depende\ de \ \theta\\&\end{align}$$Luego la función es continua en (0,0)
Saludos
;)
;)
;)
El teorema del sándwich lo aplicaría para acotar la función en polares:
$$\begin{align}&\Bigg |f_1(x,y)-0\Bigg|=\Bigg |\frac{|r|^\frac 3 2·\cos(2 \theta)}{\sqrt {\cos \theta+sen \theta}} \Bigg|=\\&\\&\Bigg |\frac{|r|^\frac 3 2·\cos(2 \theta)\sqrt {\cos \theta - sen \theta}}{\sqrt {\cos \theta+sen \theta}·\sqrt {\cos \theta - sen \theta}} \Bigg|=\\&\\&\Bigg |\frac{|r|^\frac 3 2·\cos(2 \theta)\sqrt {\cos \theta - sen \theta}}{\sqrt {\cos^2 \theta - sen^2 \theta}} \Bigg|=\\&\\&\Bigg |\frac{|r|^\frac 3 2·\cos(2 \theta)\sqrt {\cos \theta - sen \theta}}{\sqrt {\cos(2 \theta)}} \Bigg|=\\&\\&\Bigg |{|r|^\frac 3 2·\sqrt{\cos(2 \theta)}·\sqrt {\cos \theta - sen \theta}}{} \Bigg|=\\&\\&Usaré \ la \ identitat \ trigonométrica:\\&\sin( \frac {\pi} 4- \alpha)=\sin \frac {\pi} 4cos \alpha-\cos \frac {\pi} 4 \sin \alpha= \frac{\sqrt 2} 2(\cos \alpha - \sin \alpha)\ \===>\\&\\&\cos \alpha -\sin \alpha = \frac 2{\sqrt 2} \sin( \frac {\pi} 4-\alpha)= \sqrt 2 \sin( \frac {\pi} 4-\alpha)\\&\\&\Bigg |{|r|^\frac 3 2·\sqrt{\cos(2 \theta)}·\sqrt {\cos \theta - sen \theta}}{} \Bigg|=\Bigg |{|r|^\frac 3 2·\sqrt{\cos(2 \theta)}·\sqrt { \sqrt 2 \sin( \frac {\pi} 4-\alpha)}}{} \Bigg|=\\&\\&\\&\Bigg |{|r|^\frac 3 2·\sqrt{\cos(2 \theta)}· \sqrt[4] 2 ·\sqrt { \sin( \frac {\pi} 4-\alpha)}}{} \Bigg|\leq |r|^\frac 32 ·1· \sqrt[4] 2·1\\&\\&\lim_{r \to 0} |r|^\frac 32 ·1· \sqrt[4] 2·1=0\\&\\&\\&\\&\end{align}$$Donde ahora podemos concluir totalmente que ese límite vale 0 y la función es continua en (0,0)
SAludos
;)
;)
;)
Donde pone alfa y theta es lo mismo
;)
;)
