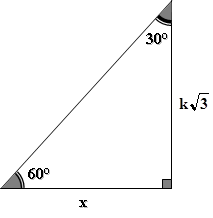
Si se tiene la longitud del cateto mayor, de un triángulo de 30°, 60° y 90°
Geometría
Resuelve el siguiente problema
Si se tiene la longitud del cateto mayor, de un triángulo de 30°, 60° y 90°, ¿cómo se obtiene la longitud del cateto menor?
3 Respuestas
Respuesta de antoniomallo
1
El lado opuesto al ángulo mayor (60º) es el cateto mayor, y el lado opuesto al ángulo menor (30º) es el cateto menor. Por supuesto, el lado opuesto al ángulo de 90º es la hipotenusa.
Teniendo en cuenta las relaciones trigonométricas,
tan 30 = cateto menor / cateto mayor
de donde
cateto menor = cateto mayor x tan 30
Donde digo el ángulo mayor o menor, obviamente estoy hablando de los dos ángulos agudos.
Respuesta de Lucas m
1
;)
Hola karla!
El cateto menor se encuentra enfrente del ángulo menor.
La razón trigonométrica que relaciona los dos catetos es la tangente:
$$\begin{align}&tan30º=\frac{cateto\ opuesto}{cateto \ contiguo}=\frac{ cateto \ menor}{cateto \ mayor}\\&\\&cateto\ menor=cateto\ mayor\times tan30º=cateto\ mayor\times \frac { \sqrt 3} 3\end{align}$$saludos
;)
;)
