Como resuelvo la ecuacion diferencial separable y`=sen(x+y)-1

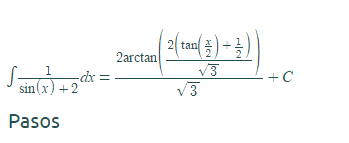
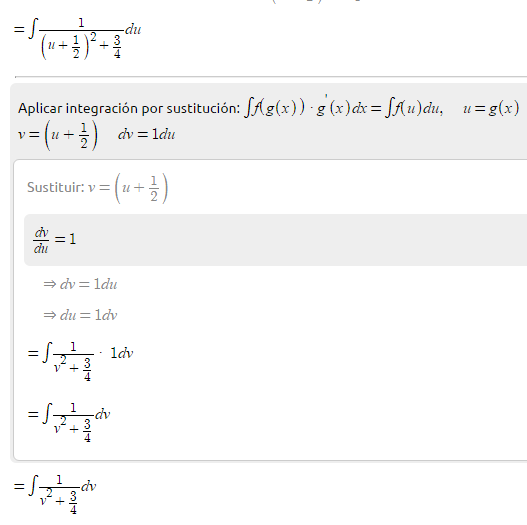
Tenemos que aplicar una reducción a sepración de variables, para eso, consideramos una sustitución,

$$\begin{align}&\displaystyle u=x+y\\&\textrm{derivamos respecto de equis,}\\&\frac{du}{dx}=1+\frac{dy}{dx}\\&\textrm{Despejamos el diferencial de ye respecto de equis,}\\&\frac{dy}{dx}=\frac{du}{dx}-1\\&\\&\end{align}$$

entonces podemos expresar la ecuación diferencial así,

$$\begin{align}&\frac{du}{dx}-1=\sin(u)-1\\&\frac{du}{dx}=\sin(u)\\&\frac{du}{\sin(u)}=dx\\&\textrm{integramos a ambos lados:}\\&\int{\frac{1}{\sin(u)}}du=\int{dx}\\&\textrm{la primera integral sería bueno que la demuestres, te queda}\\&\ln\left|\tan\left(\frac{x+y}{2}\right)\right|=x+C\\&\textrm{elevamos todo a la e potencia:}\\&e^{\ln\left|\tan\left(\frac{x+y}{2}\right)\right|}=e^{x}+e^{C}\\&\tan\left(\frac{x+y}{2}\right)=e^{x}+K\\&\textrm{si queremos obtener la solución explícita, debemos usar identidades tringonmétricas y nos queda}\\&y=2\cot^{-1}(e^{K-x})-x_{\blacksquare}\end{align}$$

y eso sería todo espero te sirva y si tienes alguna duda me avisas

;) Vaya, es más fácil de lo que pensaba, puse mal el signo del 1:

$$\begin{align}&\frac{du}{dx}-1=\sin(u)-1\\&\frac{du}{dx}=\sin(u)\\&\frac{du}{\sin(u)}=dx\\&\textrm{}\\&\int{\frac{1}{\sin(u)}}du=\int{dx}\\&\textrm{}\\&\ln\left|\tan\left(\frac{x+y}{2}\right)\right|=x+C\\&\textrm{}\\&e^{\ln\left|\tan\left(\frac{x+y}{2}\right)\right|}=e^{x}+e^{C}\\&\tan\left(\frac{x+y}{2}\right)=e^{x}+K\\&\textrm{}\end{align}$$

saludos

;)

;)