Como analizar la función para poder graficar
La función por partes es
$$\begin{cases}
x^2-3 \ \ si \ \ 0 \leq \ \ x \ { <} \ \ 2 \\
\\
-x+3 \ \ si \ \ 2 \ \leq \ \ x \leq \ 4
\end{cases}$$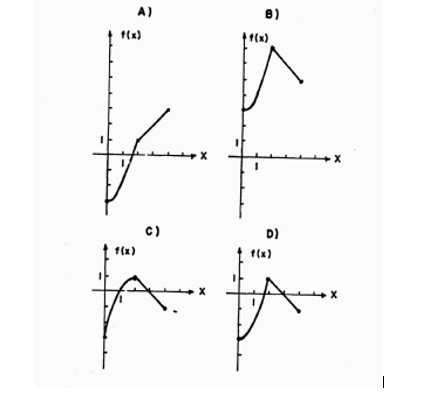
1 respuesta
;)
Hola Gabriel!
Nosotros llamamos a eso una función a trozos:
Un trozo es una parábola cóncava desplazada hacia abajo tres unidades (x^2-3)
y el otro trozo es una recta de pendiente negativa (-x+3) m=-1
Luego es la D
La función y=x^2 es una parábola cóncava (hacia arriba U) con vértice en (0,0)
y=x^2-3 es la misma parábola desplazada hacia abajo tres unidades
Saludos
;)
;)
;)
Las funciones cuadráticas:
$$\begin{align}&y=ax^2+bx+c\end{align}$$son parábolas.
Si a>0 son cóncavas (hacia arriba) en forma de U
Si a<0 son convexas (hacia abajo) en forma
$$\begin{align}&\cap\end{align}$$;)
Lucas m muchas gracias, y por que tomas el valor de -3 ?
;)
Para explicarte que a una función cualquiera y=f(x)
Si le restas un número su gráfica se traslada hacia abajo tres unidades
La función cuadrática más simple es y=x^2 que es U con vértice en (0,0)
Y=x^2-3 tiene el vértice en(0,-3). Mira la parábola del D
;)
Ahorita que he estado profundizando más sobre el tema.
Para la primera: la X toma valores desde 0 hasta 2
pAra la segunda: la X toma valores desde 2 hasta 4
En el primer caso me dan coordenadas (0,-3), (1,-2),(2,-1)
y para el segundo (2,-1) , (3,0), (4, -1)
Lucas m ... graficando me da diferente :(
;) En el primer caso también sale (2,1)
2^2-3=1
Es el punto donde coinciden recta y parábola;)
;)
