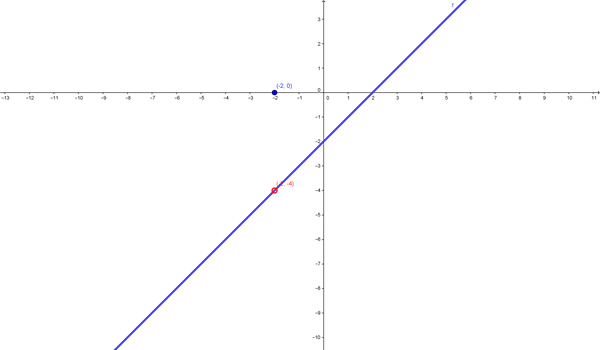
Halla gráfica de la función definid por f(x)
$$\begin{cases}
{x^2-4\over x+2}\ , & \mbox{si } x \not =-2 \\
\\
0, & \mbox{si } x = -2
\end{cases}$$
1 respuesta
;)
Hola Gabriel!
No tengo ahora el ordenador a mano y desde el móvil no puedo adjuntar gráficas.
Eso es una función con dos trozos:
La fracción que sirve para todo los valores diferentes de -2
Y un punto que es para x=-2 ==> f(-2)=0 ==> (-2,0)
Analicemos la fracción, se puede simplificar (x^2-4)/(x+2)= (x+2)(x-2)/(x+2)=x-2
Luego la gráfica de la función es una recta (y=x-2) de pendiente 1 y que corta al eje Y en -2. Pero esa recta tiene un punto vacío en (-2,-4). Y hay un punto suelto (-2,0)
;)
Es lo que se llama una Discontinuidad Evitable
;)
;)
Saludos
Bien escrita ! La función en Latex
;)
;)
¿Muchas gracias por la gráfica Lucas m y por ejemplo como dice que para POR debe ser diferente de cero por consecuencia puedo tomar un valor como -1 o -3 y también se cumple?
Diferente de -2 perdón
;)
Bueno en realidad si solo tuvieras la fracción quedaría el punto vacío y ya esta.
En este caso ese punto que no está definido, te lo redefine arbitrariamente con el valor
f(x)=0 si x=-2 ==> f(-2)=0 ==> (-2,0)
Saludos
;)
;)
