No logro terminar una tarea de derivadas
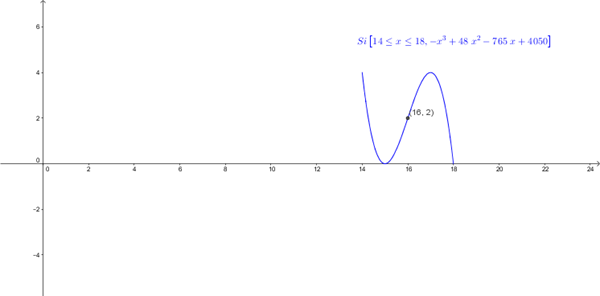
$$\begin{align}&y=-x^3+48x^2-765x+4050\end{align}$$x=Tiempo.en.horas
y=velocidad.En.decenas.de.km/h
Domimio=[14,5;18]
a) Según el dominio, en que momento inicia la marcha y en que momento llega a destino.
b) Halla primera derivada y en base a ella estudio de intervalos de crecimiento y decrecimiento y en que momento alcanzó la velocidad máxima y mínima.
c) Halla la segunda derivada y en base a ella halla los posibles puntos de inflexión
1 Respuesta
Respuesta de Lucas m
1
a) empieza en x=14 horas
y llega a destino en x=18 horas
b)
$$\begin{align}&y'=-3x^2+96x-765\\&\\&y'=0\\&\\&-3x^2+96x-765=0\\&\\&x=\frac {-96 \pm \sqrt{ 96^2-4(-3)(-765)}}{2(-3)}=\frac{-96 \pm \sqrt {36}}{-6}=\\&x_1= \frac{-90}{-6}=15\\&\\&x_2=\frac{-102}{-6}=17\\&\\&intervalos:\\&(14,15)\ ==>y'=(14.5)-3(14.5)^2+96(14.5)-765<0==>decreciente\\&(15,17)\ ==> \ y'(16)=·······sustituye>0\ ==>creciente\\&(17,18) ==>\ y'(17.5)<0==> decreciente\\&velocidad\ minima \ a \ las \15 \ horas==>v(15)=y(15)=sustituye···=0\\&\\&velocidad\ máxima \ a \ las \ 17 \horas ==>v(17)=y(17)=sustituye··=4\ decenas \ km/h \equiv40km/h\\&\\&c)punto \ inflexión\\&y''=0\\&y''=-6x+96=0\\&\\&x=16 ==>(16,y(16))=(16,2)\end{align}$$gráfica
Saludos
;)
;)
¡Gracias!
;)
Empieza en 14.5
;)
