Un pino mide 30 m de altura más que otro. Un observador que está a 100 m de distancia del pino más bajo
Geometría: Trigonometría
Un pino mide 30 m de altura más que otro. Un observador que está a 100 m de distancia del pino más bajo, observa las puntas de ellas en una misma dirección con un ángulo de elevación de 30°. Determinar las alturas de los pinos y la distancia entre ellos.
2 respuestas
Como estas:
Se tiene el siguiente gráfico:
Las barras sombreadas representan los pinos.
En el triángulo rectángulo CDE, hallamos "X" (Distancia entre los pinos)
En el triángulo rectángulo ABC, hallamos "H" (Altura del pino más bajo)
Altura del pino más bajo: 58 m
Altura del pino más alto: 58 m + 30 m = 88 m
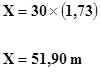
1. Altura de los pinos
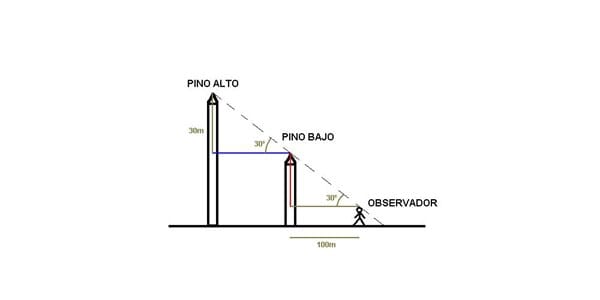
Se forma un triángulo cuyos vértices son los ojos del observador, la punta del pino bajo y la parte inferior del pino bajo que está a la altura de los ojos del observador.
Los lados de dicho triángulo son:
Parte de la línea discontinua (comienza en los ojos del observador y termina en la punta del pino bajo)
Línea roja (comienza en la punta del pino bajo y termina en la parte inferior del pino bajo que está a la altura de los ojos del observador)
Línea verde (comienza en la parte inferior del pino bajo que está a la altura de los ojos del observador y termina en los ojos del observador)
Consideramos:
La hipotenusa (Parte de la línea discontinua)
Cateto opuesto (Línea roja)
Cateto adyacente (Línea verde)
Usaremos la siguiente razón trigonométrica
tangente del ángulo = cateto opuesto / cateto adyacente
El cateto opuesto es lo que vamos a determinar, entonces nos queda:
cateto opuesto = tangente del ángulo x cateto adyacente
cateto opuesto = tangente de 30º x 100m = 58m
Altura del pino bajo = 58m + la altura del observador
Altura del pino alto = 58m + 30m + la altura del observador
2. Distancia entre los pinos
Se forma otro triángulo cuyos vértices son la punta del pino bajo, la punta del pino alto y la parte del pino alto que está a la altura de la punta del pino bajo.
Los lados de dicho triángulo son:
Parte de la línea discontinua (comienza en la punta del pino bajo y termina en la punta del pino alto)
Línea verde (comienza en la punta del pino alto y termina en la parte del pino alto que está a la altura de la punta del pino bajo)
Línea azul (comienza en la parte del pino alto que está a la altura de la punta del pino bajo y termina en la punta del pino bajo)
Consideramos:
La hipotenusa (Parte de la línea discontinua)
Cateto opuesto (Línea verde)
Cateto adyacente (Línea azul)
Usaremos la misma razón trigonométrica de la parte 1
tangente del ángulo = cateto opuesto / cateto adyacente
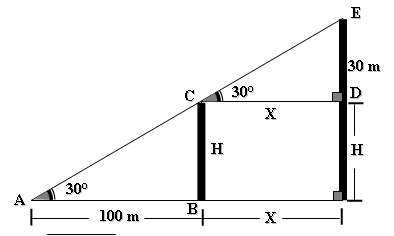
El cateto adyacente es lo que vamos a determinar, entonces nos queda:
cateto adyacente = cateto opuesto / tangente del ángulo
cateto adyacente =30m / tangente de 30º= 52m
Distancia entre los pinos = 52m
EN RESUMEN
ALTURA DEL PINO BAJO = 58m + ALTURA DEL OBSERVADOR
ALTURA DEL PINO ALTO = 88m + ALTURA DEL OBSERVADOR
DISTANCIA ENTRE LOS PINOS =52m