Así soluciono para saber si es con-tinua o dis-continua la siguiente función, correcccion

La función es

$$\begin{cases}
x-4, \ \ \ si -2< x <2 \\ 
\\
x^2 , \ \ \ si  \ \ \ 2 <  x \leq 4
\end{cases}$$

la grafica de esta funcion es

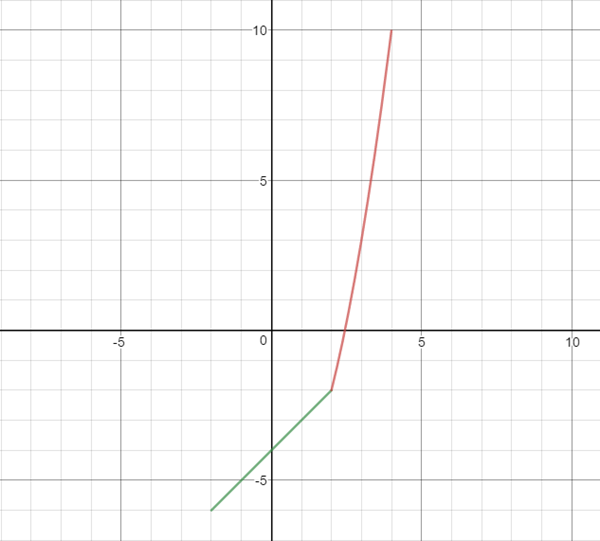
para mi solucion:

$$\begin{align}&la \ \  condicion \ \  es \ \  que \ \  \\&f(2)=\lim_{x \to 2}f(x)\end{align}$$

en este caso tomo el 2 para hacer la condición,  por que esta en el "centro", eso esta bien, o debo poner 4 porque en este caso es el que se incluye (menor o igual a 4 por la función a trozos)

$$\begin{align}&la \ \  funcion \ \ f(2) = x^2-6 = -2\\&cuando \ \ se \  aproxima\ \ por  \ la \ \ izquierda\lim_ {x \to \  2} \ x-4 = -2\\&cuando \ \ se \  aproxima\ \ por  \ la \ \ derecha\lim_ {x \to \  2} \ x^2-6 = -2\\&\\&SEGUN \ \ yo, \ \ veo \ que \  se \ \ cumple \ \ por \ \ consecuencia \ es \ continua \  en \\&x=2, \\&pero \ \ la \ solucion \ \ dice \ \  que \ \  es \ \ discontinua \ \ en \ \ x =2\\&\\&AYUDA.\end{align}$$