Como se calcula el área bajo la curva

;)
Hola Gabriel!

El área bajo una curva, comprendida por la curva y el eje x, se calcula con el valor absoluto de la integral definida .

Si la función cambia de signo, hay que calcular el área de cada recinto por separado.

Para ver si esto ocurre, primero calculamos los puntos de corte de la función con el eje OX (abscisas) ==>  y=0 ==>

$$\begin{align}&x^3+3x^2+2x=0\\&\\&x(x^2+3x+2)=0\\&x=0\\&x^2+3x+2=0\\&==>\\&x=-1\\&x=-2\end{align}$$

Hay tres puntos de corte y como me piden el área desde x=-3 a x=3, que quedan fuera de esos puntos tendremos 4 recintos: en los intervalos:

[-3,-2]

[-2,-1]

[-1,0]

[0,3]

En cada uno de ellos hay que hacer la integral definida y sumar sus valores absolutos:

Te planteo las integrales definidas y espero sepas hacer los cálculos:

$$\begin{align}&\int_{-3}^{-2}(x^3+3x^2+2x)dx=\frac{x^4} 4+x^3+x^2 \Bigg]_{-3}^{-2}=\\&\\&\frac{(-2)^4}4+(-2)^3+(-2)^2-\Bigg(\frac{(-3)^4}4+(-3)^3+(-3)^2\Bigg)=-\frac 9 4\\&\\&\int_{-2}^{-1}(x^3+3x^2+2x)dx=\frac{x^4} 4+x^3+x^2 \Bigg]_{-2}^{-1}=operando=\frac 1 4\\&\\&\int_{-1}^{0}(x^3+3x^2+2x)dx=\frac{x^4} 4+x^3+x^2 \Bigg]_{-1}^{0}=F(0)-F(-1)=operando=- \frac 1 4\\&\\&\int_{0}^{3}(x^3+3x^2+2x)dx=\frac{x^4} 4+x^3+x^2 \Bigg]_{0}^{3}=F(3)-F(0)=operando= \frac {225} 4\\&\\&F(x)=\int f(x)dx=\frac{x^4} 4+x^3+x^2\\&\\&Area=\frac 9 4+ \frac 1 4+ \frac 1 4+ \frac {225}4=59 \ u^2\\&\\&\end{align}$$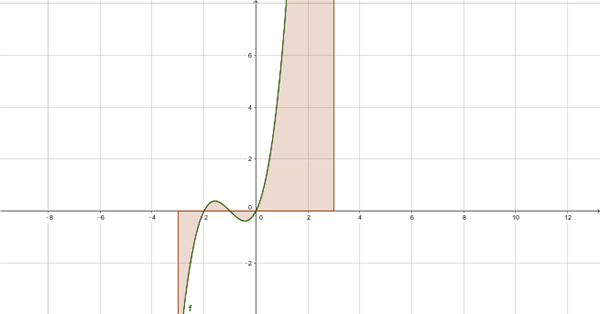

Saludos

;)

;)