Encuentre la ecuación del círculo que pasa por los puntos z_1=-2+2i,z_2=2-2i,z_3=2

;)
Hola IGNAcio!

Estamos buscando la circunferencia circunscrita al triángulo definido por esos tres complejos.

Hemos de buscar el circumcentro de forma análoga a como ya te hice el otro.

Después buscaremos el radio( distancia del circumcentro a uno de esos vértices)

$$\begin{align}&z_1=-2+2i\\&z_2=2-2i\\&z_3=2\\&\\&mediatriz\ z_1z_3\\&|z-z_3|=|z-z_1|\\&\\&|x+iy-2|=|x+iy+2-2i|\\&\\&|(x-2)+yi|=|(x+2)+(y-2)i|\\&\\&(x-2)^2+y^2=(x+2)^2+(y-2)^2\\&\\&x^2-4x+4+y^2=x^2+4x+4+y^2-4y+4\\&0=8x-4y+4\\&2x-y+1=0\\&\\&mediatriz\ z_2z_3\\&|z-z_3|=|z-z_2|\\&|x+yi-2|=|x+iy-2+2i|\\&\\&|(x-2)+yi|=|(x-2)+(y+2)i|\\&(x-2)^2+y^2=(x-2)^2+(y+2)^2\\&\\&y^2=(y+2)^2\\&y^2=y^2+4y+4\\&y=-1\\&\\&\text{ resolviendo el sistema}\\&2x-y+1=0\\&y=-1\\&==>\\&x=-1\\&Circumcentro=(-1,-1)=-1-i\\&\\&r=|z-z_3|=|(-1-i)-2|=|-3-i|=\sqrt{(-3)^2+(-1)^2}= \sqrt {10}\\&\\&circunferencia:\\&(x+1)^2+(y+1)^2=10\end{align}$$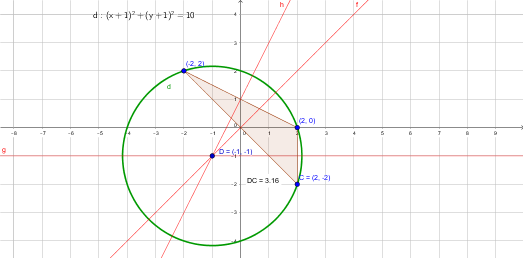

Saludos

;)

;)