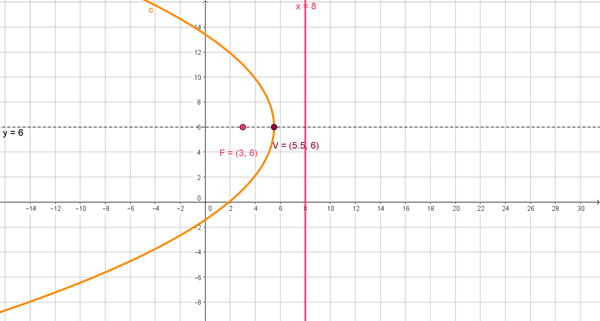
en resumen, seria de la siguiente manera
Parabola horizontal, con vertice en (h,k)
$$\begin{align}&\longrightarrow horizontal, \ abre \ ramas \ izquierda\\&(y-k)^2=-4p(x-h)\\&V(h,k)\\&F(h-p,k)\\&x=h-p\\&\\&\longrightarrow horizontal, \ abre \ ramas \ derecha\\&(y-k)^2=4p(x-h)\\&V(h,k)\\&F(h+p,k)\\&x=h-p\\&\\&.............................................\end{align}$$Parabola vertical, con vertice en (h,k)
$$\begin{align}&\longrightarrow vertical, \ abre \ ramas \ hacia \ abajo\\&(x-h)^2=-4p(y-k)\\&V(h,k)\\&F(h,k-p)\\&y=k-p\\&\\&\longrightarrow vertical, \ abre \ ramas \ hacia \ arriba\\&(x-h)^2=4p(y-k)\\&V(h,k)\\&F(h,k+p)\\&y=k-p\\&\\&.............................................\end{align}$$tengo dudas en las directrices, o asi son?