Demostrar la ecuación elipse y la ecuación de la parábola de los siguientes ejercicios

;)
Hola oscar!
Hacemos uno de esos por pregunta. Te hago el primero.

Manda el otro en otra pregunta o espera otro Experto:

Completamos cuadrados:

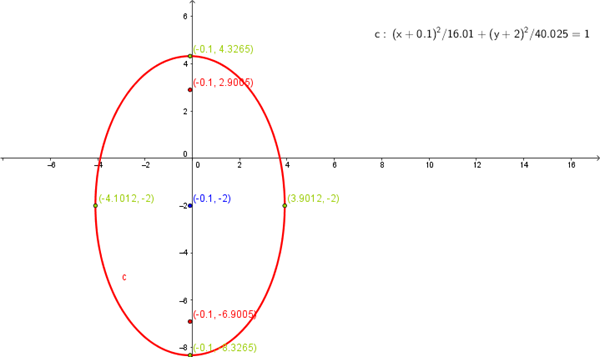
$$\begin{align}&(10x^2+2x)+(4y^2+16y)=144\\&\\&\text{dejamos el coeficiente de los cuadrados en 1}\\&10(x^2+ \frac x 5)+4(y^2+4y)=144\\&\\&\text{El binomio del que proceden es}(x+ \frac 1 2· \frac 1 5)\\&\text{es   decir x y la mitad del coeficiente de la x}:\\&(x^2+ \frac x 5)=(x+ \frac 1{10})^2- \frac 1 {100}\\&\text{y compensamos el término independiente}\\&Para\ y\\&(y^2+4y)=(y+2)^2-4\\&\\&La \ ecuación \ queda\\&10 \Big[(x+ \frac 1{10})^2- \frac 1 {100} \Big]+4 \Big[(y+2)^2-4\Big]=144\\&\\&10(x+ \frac 1 {10})^2- \frac{10}{100}+4(y+2)^2-16=144\\&10(x + \frac 1 {10})^2+4(y+2)^2=144+16+ \frac 1 {10}\\&\\&10(x + \frac 1 {10})^2+4(y+2)^2=\frac{1601}{10}\\&\text{Haciendo el término independiente 1, multiplicando toda la ecuación por:}\\&\\&\Bigg[ 10(x + \frac 1 {10})^2+4(y+2)^2=\frac{1601}{10} \Bigg] \frac{10}{1601}\\&\\&\frac{100}{1601}(x+ \frac 1 {10})^2+ \frac {40}{1601}(y+2)^2=1\\&\\&\frac{(x+ \frac 1 {10})^2}{ 16.01} + \frac { (y+2)^2}{40.025}=1\\&\\&Elipse \ Vertical\\&de Centro =( -\frac 1 {10},-2)\\&semieje \ mayor: a= \sqrt{40.025}\\&b=\sqrt{16.01}\\&\\&a^2=b^2+c^2\\&\\&c^2=a^2-b^2=40.025-16.01=24.015\\&c=\sqrt{24.015}\\&Focos:\\&F=(- \frac 1 {10},-2+c)=(- \frac 1 {10},-2+ \sqrt{24.015}) \simeq(-\frac 1 {10},2.9005)\\&F'=(- \frac 1 {10},-2-c)=(- \frac 1 {10},-2- \sqrt{24.015}) \simeq(-\frac 1 {10},-6.9005)\\&\\&Vertices\\&V=(- \frac 1 {10},-2+a)=(- \frac 1 {10},-2+ \sqrt{40.025}) \simeq(- \frac 1 {10},4.3265)\\&V'=(- \frac 1 {10},-2-a)=(- \frac 1 {10},-2- \sqrt{40.025}) \simeq(- \frac 1 {10},-8.3265)\end{align}$$

graficando:

Saludos y recuerda votar

;)

;)

¡Gracias!

Lucas un bue día y mil gracias