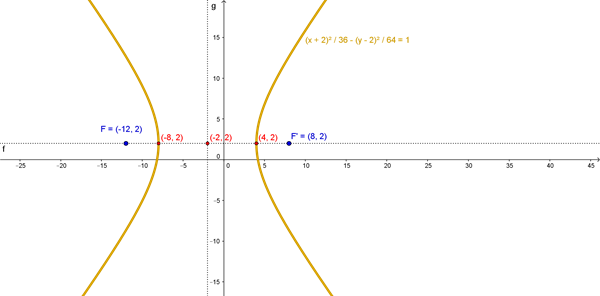
Encuentre la ecuación de la hipérbola que satisface que el centro es (-2,2), un vértice es (4,2), y un foco es (6,2)
Geometría
Encuentre la ecuación de la hipérbola que satisface que el centro es (-2,2), un vértice es (4,2), y un foco es (6,2). Dibuje la gráfica de la hipérbola encontrada.
1 Respuesta
Respuesta de Lucas m
1