Encuentre la ecuación de la parábola de eje paralelo al de coordenadas x, y que pasa por los puntos (-2,1), (1,2) y (-1,3)

;)
Hola Ume Lee!

Como el eje es paralelo al eje X, es una parábola de 2º grado en y

$$\begin{align}&x=ay^2+by+c\\&\\&\text{Sustituyendo los  puntos}\\&(-2,1)==> -2=a+b+c\\&(1,2)==>1=4a+2b+c\\&(-1,3)===>-1=9a+3b+c\\&\\&\text{Resolviendo el sistema}:\\&a=- \frac 5 2\\&\\&b= \frac {21} 2\\&\\&c=-10\\&\\&x= - \frac 5 2 y^2+ \frac{21} 2 y-10\\&\\&2x=-5y^2+21y-20\\&\\&5y^2-21y+2x=-20\\&\\&\text{completando cuadrados}\\&5(y^2- \frac {21} 5y)+2x=-20\\&\\&\text{ese binomio, viene del cuadrad}o:\\&(y^2- \frac{21} 5y)=(y- \frac{21}{10})^2- \frac {441}{100}\\&\\&luego\ la \ parábola:\\&5 \Bigg[(y- \frac{21}{10})^2- \frac {441}{100}\Bigg]+2x=-20\\&\\&5(y- \frac{21}{10})^2- \frac {441}{20}+2x=-20\\&\\&5(y- \frac{21}{10})^2=-2x+ \frac {441}{20}-20\\&\\&5(y- \frac{21}{10})^2=-2x+ \frac{41}{20}\\&\\&(y- \frac{21}{20})^2=\frac 1 5(-2x+ \frac {41}{20})\\&\\&(y- \frac{21}{10})^2=- \frac 2 5(x- \frac {41}{40})\\&\\&V=( \frac {41}{40}, \frac {21}{10})\\&\\&eje\ focal \ en \ \\&y= \frac {21}{10}\\&\\&4p=- \frac 2 5\\&\\&p=- \frac 1 {10}\\&\\&p<0\ ==> abierta \ a \ la \ izquierda\\&\\&F=(( \frac{41}{40}- \frac 1 {10}, \frac {21}{10})\\&\end{align}$$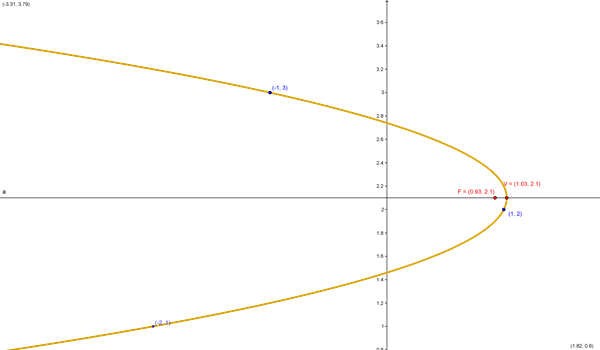

Saludos

;)

;)