Estimación de parámetros a. La estimación puntual de la media y la desviación estándar.

a) La estimación de la media se hace haciendo la media de las medidas que tenemos, así que la media es:

Xmed=(10.3+12.4+11.6+11.8+12.6+10.9+11.2+10.3)/8=11.3875

Para poder calcular la desviación estandar se necesita lo que se llama varianza (más bien su estimación) y para ello es necesaria la media. La varianza es:

$$\begin{align}&S^2=\frac{\sum_{i=0}^{n}(X_i-X_{med})^2}{n-1}\end{align}$$

La desviación estandar no es más que la raiz cuadrada de la varianza, así pues, tenemos que:

$$\begin{align}&S^2=\frac{\sum_{i=0}^{n}(X_i-X_{med})^2}{n-1}=\frac{(10.3-11.3875)^2+(12.4-11.3875)^2+(11.6-11.3875)^2+(11.8-11.3875)^2+(12.6-11.3875)^2+(10.9-11.3875)^2+(11.2-11.3875)^2+(10.3-11.3875)^2+}{8-1}=0.7641\\&S=\sqrt{S^2}=0.8741\end{align}$$

b) Para el intervalo de confianza lo primero que debemos hacer es ver cual es el riesgo de que un valor caiga fuera del intervalo de confianza, es decir, que nos de un valor que consideremos malo. Este riesgo es del 2% en este caso, es decir 1% por cada lado de la normal. Sabiendo la varianza y la probabilidad que deja por cada lado es sencillo encontrar el intervalo de confianza.

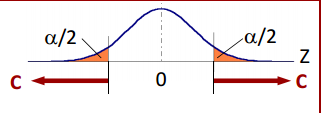
Aqui se puede ver lo que digo. Sin embargo, en este caso, la variable es Z y no nuestra X y además la media es 0. Así que se hace un cambio de escala donde modificamos nuestra variable X para que nos de en función de Z y esta la tenemos tabulada. La formula para este cambio es:

Bien, pues m es la media, X es el valor que buscamos y sigma es nuestra S desviación estandar.

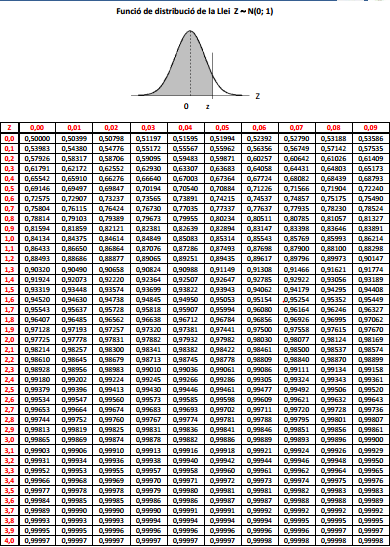
En las tablas de la ley normal buscamos un valor muy cercano a 0.99 y vamos al valor de Z que nos da, por la izquierda 2.3 y por arriba 0.03 por lo tanto nuestro valor límite de Z por arriba será 2.33. Y aplicando la formula tenemos el limite de confianza superior. Cabe recordar que como es simetrico, solo debemos cambiar el signo de la Z para encontrar el límite inferior.

$$\begin{align}&Z=\frac{X-m}{\sigma}\\&X_{sup}=Z\sigma+m=2.33·0.8741+11.3875=13.42\\&X_{inf}=-Z\sigma+m=11.3875-2.33·0.8741=9.35\end{align}$$

Quizá escrito de esta forma se ve mejor la relación entre la X y la Z. Vemos que sumando la m estamos descentrando la X del 0 y si multiplicamos la Z lo que hacemos es que la curva sea mas plana o mas estirada.

Si tienes alguna duda no dudes en contactar conmigo. Salu2.