¿Que probabilidad es y como se resuelve?
Hay un ejercicio que intento de resolver pero no se que probabilidad es, si es la Poisson, Binomial o Hipergeometrica. Tampoco se muy bien como se resuelve en este caso
Por una esquina de la Capital Federal transitan en promedio 15 autos por minuto. Se desea calcular la probabilidad de que:
a) En un minuto pasen exactamente 11 autos
b) En un minuto pasen más de 12 autos.
c) Durante 30 segundos pasen 7 automóviles.
1 Respuesta
;)
;)
Hola h Ituarh!
La distribución de Poisson se usa en dos casos:
Cuando se producen sucesos independientes en una determinada cantidad de tiempo y conocemos la media de los que suceden.
Cuando se producen sucesos en una cantidad de superficie, línea o espacio.
Lo importante es que son sucesos independientes, la probabilidad de que sucedan es independiente de la cantidad de sucesos habidos antes.
Tiene un parámetro lambda que indica la cantidad de sucesos esperados en el tiempo o superficie que estamos estudiando. Su función de probabilidad es esta:
$$\begin{align}&P(k)=\frac{e^{- \lambda} \lambda ^k}{k!}\\&\\&donde \ \ \lambda \ \ es \ el \ número \ de \ sucesos \ esperados \ en \ el \ intervalo \ de \ tiempo \ de \ estudio.\\&\\&\lambda=15 \ \ autos / minuto\\&\\&\\&P(11)=\frac{e^{- 15} 15 ^{11}}{11!}=0.0663\\&\\&b)\\&P(x>12)=1-\Bigg[P(x=0)+P(x=1)+P(x=2)+······+P(x=12)\Bigg]=1-0.2676=0.7324\\&\text{has de aplicar esa fórmula trece veces}\\&\\&\\&\\&\\&\end{align}$$Lo he calculado con GeoGebra:
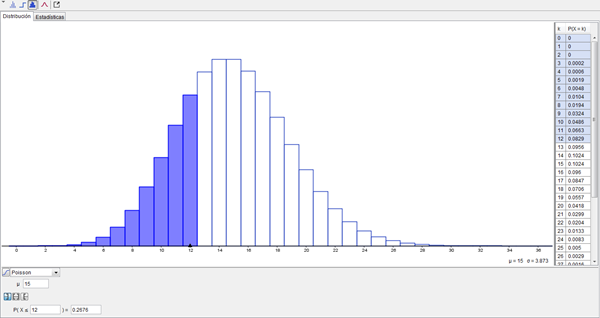
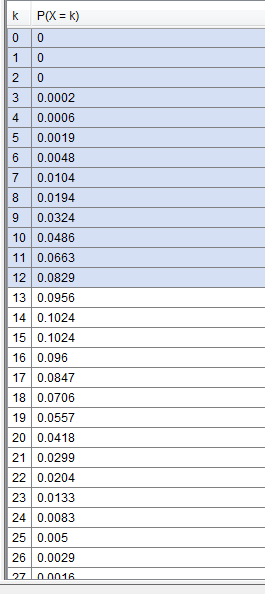
c)
El periodo son 30 segundos
$$\begin{align}&\lambda=7.5\\&P(k)=\frac{e^{- \lambda} \lambda ^k}{k!}\\&\\&P(7)=\frac{e^{-7.5}·7.5^7}{7!}=0.1465\end{align}$$Saludos y recuerda votar
;)
;)
