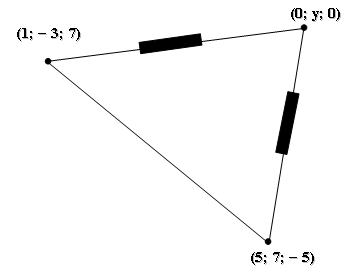
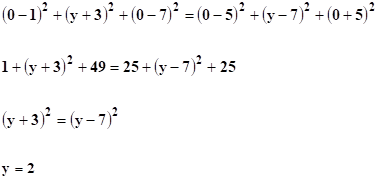Encuentra un tercer punto de la forma (0, y, 0) tal que forme un triángulo isósceles en el espacio con los puntos (1, -3, 7)
Geometría analítica
Encuentra un tercer punto de la forma (0, y, 0) tal que forme un triángulo isósceles en el espacio con los puntos (1, -3, 7) y (5, 7, -5)
2 respuestas
Respuesta de Luis Alberto Candio Salcedo
1
Respuesta
1