Para la siguiente función, Realiza la gráfica
- Determine la ordenada al origen
- Calcula los límites cuando “x” tiende a 2
- Explica si la función es continua precisamente en𝑥 = 2 y porqué es o no continua
- f(x)=x-3 si x>2
- f(x)=3-2x si x<2
1 respuesta
;)
Hola Lisset!
A simple vista se ve que no es contínua, porque aunque son dos trozos de recta, la función no está definida en x=2.
$$\begin{align}&f(2)= \not \exists\\&\\&\lim_{x \to 2^-}(x-3)=2-3=-1\\&\\&\lim_{x \to 2^+}(3-2x)=3-4=-1\\&\\&\text{luego tiene límite en x=2}\\&\\&\lim_{x \to 2} f(x)=\lim_{x \to 2^-} f(x)=\lim_{x \to 2^+} f(x)=-1\end{align}$$Para que una función sea continua en un punto ha de cumplir tres condiciones:
1) Que exista la imagen en ese punto . En este caso no hay f(2)
2) Que tenga límite en ese punto. En este caso si lo cumple ya que los límites laterales son iguales
3) Que la imagen y el límite coincidan
$$\begin{align}&\lim_{x \to 2} f(x)=f(2)\end{align}$$En este caso al no haber f(2) esto es imposible.
La función presenta una Discontinuidad, llamada Evitable, en x=2
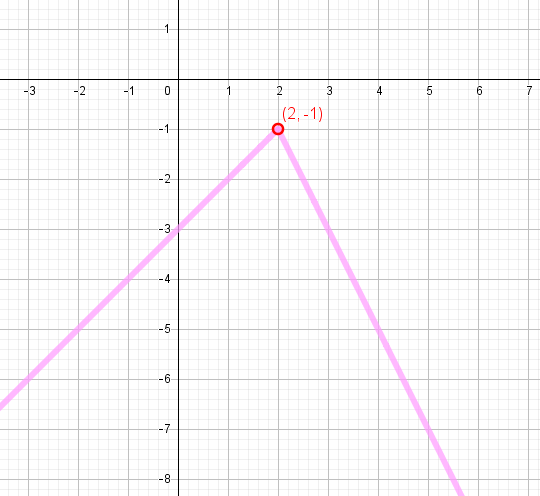
El punto (2,-1) no pertenece a la función, no está definido . Está hueco:
Recuerda votar las respuestas, Excelente si quieres nuevas contestaciones mías
Saludos
;)
;)
||*||
Tengo una duda, y para graficarla, ¿se utilizan los resultados de los límites?
;)
El límite en x=2 te indica el punto donde se juntarían las dos rectas (2,-1)
;)
